Nội dung từ Loigiaihay.Com
Câu hỏi:
Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có đường phân giác trong \(AD\) và đường cao \(CH\) lần lượt có phương trình \(x + y - 2 = 0,\) \(x - 2y + 5 = 0\). Điểm \(M\left( {3;\,\,0} \right)\) thuộc \(AC\) thỏa mãn \(AB = 2AM\). Tọa độ các đỉnh của tam giác \(ABC\) lần lượt là:
- A \(A\left( {1;\,\,1} \right),\,\,B\left( {3;\,\, - 3} \right),\,\,C\left( { - 1;\,\,2} \right)\)
- B \(A\left( {1;\,\,1} \right),\,\,B\left( {3;\,\,3} \right),\,\,C\left( { - 1;\,\,2} \right)\)
- C \(A\left( {1;\,\, - 1} \right),\,\,B\left( {3;\,\, - 3} \right),\,\,C\left( { - 1;\,\,2} \right)\)
- D \(A\left( { - 1;\,\,1} \right),\,\,B\left( {3;\,\, - 3} \right),\,\,C\left( { - 1;\, - \,2} \right)\)
Phương pháp giải:
+) Gọi \(E\) là điểm đối xứng với \(M\) qua \(AD\)\( \Rightarrow E \in AB\)
+) Có \(CH\) là đường cao, viết được phương trình cạnh \(AB.\) Xác định tọa độ đỉnh \(A\). Từ đó, xác địnhh được tọa độ đỉnh \(B,\,\,C.\)
Lời giải chi tiết:
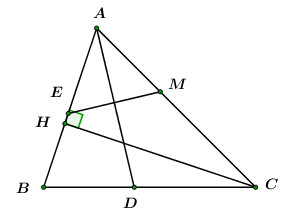
+) Gọi \(E\) là điểm đối xứng với \(M\) qua \(AD\)\( \Rightarrow E \in AB\) và \(E\left( {2;\,\, - 1} \right)\)
+) Phương trình đường cao \(\left( {CH} \right):\,\,x - 2y + 5 = 0 \Rightarrow {\vec n_{CH}} = \left( {1;\,\, - 2} \right) \Rightarrow {\vec u_{CH}} = \left( {2;\,\,1} \right)\)
+) Phương trình cạnh \(\left( {AB} \right):\left\{ \begin{array}{l}{\rm{qua}}\,\,E\left( {2;\,\, - 1} \right)\\{{\vec n}_{AB}} = {{\vec u}_{CH}} = \left( {2;\,\,1} \right)\end{array} \right.\)
\( \Rightarrow AB:\,\,\,2\left( {x - 2} \right) + y + 1 = 0\)\( \Leftrightarrow 2x - 4 + y + 1 = 0\)\( \Leftrightarrow 2x + y - 3 = 0\)
+) \(A = AB \cap AD\)\( \Rightarrow \) Tọa độ điểm \(A\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + y - 2 = 0\\2x + y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right. \Rightarrow A\left( {1;\,\,1} \right)\)
+) Gọi \(B\left( {t;\,\,3 - 2t} \right);\,\,A\left( {1;\,\,1} \right);\,\,M\left( {3;\,\,0} \right)\)
\( \Rightarrow AB = \sqrt {{{\left( {t - 1} \right)}^2} + {{\left( {2 - 2t} \right)}^2}} \) và \(AM = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {0 - 1} \right)}^2}} = \sqrt {4 + 1} = \sqrt 5 \)
Theo đề bài, \(AB = 2AM\)\( \Rightarrow \sqrt {{{\left( {t - 1} \right)}^2} + {{\left( {2 - 2t} \right)}^2}} = 2\sqrt 5 \)\( \Leftrightarrow \sqrt {{{\left( {t - 1} \right)}^2} + 4{{\left( {t - 1} \right)}^2}} = 2\sqrt 5 \)
\( \Leftrightarrow \sqrt 5 .\left| {t - 1} \right| = 2\sqrt 5 \Rightarrow \left[ \begin{array}{l}t - 1 = 2\\t - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = - 1\end{array} \right.\)
\( \Rightarrow B\left( {3;\,\, - 3} \right)\) hoặc \(B\left( { - 1;\,\,5} \right)\)
Mặt khác, \(AB = 2AM\)\( \Rightarrow E\) là trung điểm của \(AB\)\( \Rightarrow B\left( {3;\,\, - 3} \right)\)
Phương trình đường thẳng \(AC\) đi qua \(A\left( {1;\,\,1} \right)\) và \(M\left( {3;\,\,0} \right)\) là:
\(AC:\,\,\,\frac{{x - 1}}{{3 - 1}} = \frac{{y - 1}}{{0 - 1}} \Leftrightarrow x - 1 + 2y - 2 = 0\) \( \Leftrightarrow x + 2y - 3 = 0.\)
Tọa độ điểm \(C\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x + 2y - 3 = 0\\x - 2y + 5 = 0\end{array} \right. \Rightarrow C\left( { - 1;\,\,2} \right)\)
Vậy \(A\left( {1;\,\,1} \right),\,\,B\left( {3;\,\, - 3} \right),\,\,C\left( { - 1;\,\,2} \right).\)
Chọn A.













