Nội dung từ Loigiaihay.Com
Câu hỏi:
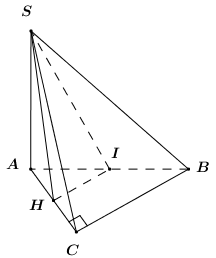
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tamm giác vuông cân tại \(C\), \(AB = 2a\), \(SA \bot \left( {ABC} \right)\), \(SA = a\). Gọi \(I,\,\,H\) lần lượt là trung điểm của các cạnh \(AB\) và \(AC\). Cosin của góc giữa hai mặt phẳng \(\left( {SIH} \right)\) và \(\left( {SBC} \right)\) là:
- A \(\cos \alpha = \dfrac{{\sqrt 3 }}{{10}}\)
- B \(\cos \alpha = \dfrac{{2\sqrt 2 }}{3}\)
- C \(\cos \alpha = \dfrac{{\sqrt 5 }}{3}\)
- D \(\cos \alpha = \dfrac{{3\sqrt {10} }}{{10}}\)
Phương pháp giải:
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Áp dụng định lí Pytago trong tam giác vuông và định lí cosin trong tam giác.
Lời giải chi tiết:
Xét \(\left( {SIH} \right)\) và \(\left( {SBC} \right)\) có:
\(\left\{ \begin{array}{l}S \in \left( {SIH} \right) \cap \left( {SBC} \right)\\IH \subset \left( {SIH} \right);\,\,BC \subset \left( {SBC} \right)\\IH\parallel BC\end{array} \right.\)\( \Rightarrow \left( {SIH} \right) \cap \left( {SBC} \right) = d\) với \(d\) là đường thẳng qua \(S\) và song song với \(IH,\,\,BC\).

Ta có: \(\left\{ \begin{array}{l}BC \bot AC\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC\).
Mà \(BC\parallel d \Rightarrow SC \bot d\).
Ta có \(IH\parallel BC,\,\,BC \bot \left( {SAC} \right)\)\( \Rightarrow IH \bot \left( {SAC} \right) \Rightarrow IH \bot SH\).
Mà \(IH\parallel d \Rightarrow SH \bot d\).
Ta có: \(\left\{ \begin{array}{l}\left( {SIH} \right) \cap \left( {SBC} \right) = d\\\left( {SIH} \right) \supset SH \bot d\\\left( {SBC} \right) \supset SC \bot d\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {SIH} \right);\left( {SBC} \right)} \right) = \angle \left( {SH;SC} \right) = \angle HSC = \alpha \).
Tam giác \(ABC\) vuông cân tại \(C\) có \(AB = 2a\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = a\sqrt 2 \).
\( \Rightarrow AH = HC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\).
Áp dụng định lí Pytago trong các tam giác vuông ta có:
\(\begin{array}{l}SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \\SH = \sqrt {S{A^2} + A{H^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 6 }}{2}\end{array}\)
Áp dụng định lí Cosin trong tam giác \(SHC\) ta có:
\(\begin{array}{l}\cos \angle HSC = \dfrac{{S{H^2} + S{C^2} - H{C^2}}}{{2SH.SC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{3{a^2}}}{2} + 3{a^2} - \dfrac{{{a^2}}}{2}}}{{2.\dfrac{{a\sqrt 6 }}{2}.a\sqrt 3 }} = \dfrac{{2\sqrt 2 }}{3}\end{array}\)
Vậy \(\cos \alpha = \dfrac{{2\sqrt 2 }}{3}\).
Chọn B.













