Nội dung Tổng hợp
Câu hỏi:
Một lò xo có độ cứng k, độ dài tự nhiên l0 được treo thẳng đứng, đầu trên cố định. Người ta treo quả cân có khối lượng 250 g vào đầu dưới của lò xo. Khi vật cân bằng thì lò xo có độ dài 35 cm. Nếu treo thêm quả cân 500 g nữa vào đầu dưới của lò xo thì khi vật cân bằng, lò xo dài 40 cm. Lấy g = 10 m/s2. Độ dài tự nhiên và độ cứng của lò xo là:
- A l0 = 30 cm; k = 50 N/m
- B l0 = 32 cm; k = 300 N/m
- C l0 = 32 cm; k = 200 N/m
- D l0 = 30 cm; k = 100 N/m.
Phương pháp giải:
+ Định luật Húc: Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo: \({F_{dh}} = k.\Delta l\)
+ Khi vật cân bằng thì: \(\overrightarrow {{F_{dh}}} + \overrightarrow P = \overrightarrow 0 \Rightarrow {F_{dh}} = P \Leftrightarrow k.\Delta l = mg\)
Lời giải chi tiết:
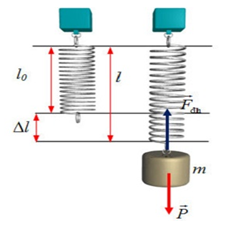
Vật nặng chịu tác dụng của:
+ Lực đàn hồi: \({F_{dh}} = k.\Delta l\)
+ Trọng lực: P = mg
Khi vật cân bằng thì: \(\overrightarrow {{F_{dh}}} + \overrightarrow P = \overrightarrow 0 \Rightarrow {F_{dh}} = P \Leftrightarrow k.\Delta l = mg\)
Khi \(m = {m_1} = 0,25kg \Rightarrow k.\Delta {l_1} = {m_1}g \Leftrightarrow k.\left( {{l_1} - {l_0}} \right) = {m_1}g \Leftrightarrow k.\left( {0,35 - {l_0}} \right) = 0,25.g\,\,\left( 1 \right)\)
Khi \(m = {m_2} = 0,5kg \Rightarrow k.\Delta {l_2} = {m_2}g \Leftrightarrow k.\left( {0,4 - {l_0}} \right) = 0,5.g\,\,\left( 2 \right)\)
\(\begin{array}{l}\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}} \Rightarrow \dfrac{{0,35 - {l_0}}}{{0,4 - {l_0}}} = \dfrac{{0,25}}{{0,5}} \Rightarrow {l_0} = 0,3m = 30cm \Rightarrow \Delta {l_1} = 0,35 - 0,3 = 0,05m\\ \Rightarrow k = \dfrac{{{m_1}g}}{{\Delta {l_1}}} = \dfrac{{0,25.10}}{{0,05}} = 50N/m\end{array}\)
Chọn A.













