Nội dung từ Loigiaihay.Com
Câu hỏi:
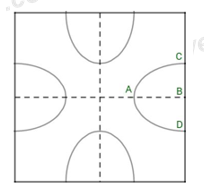
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh \(20cm\) bằng cách khoét đi bốn phần bằng nhau có hình dạng một nửa elip như hình bên. Biết một nửa trục lớn\(AB = 6cm\) , trục bé \(CD = 8cm\) . Diện tích bề mặt hoa văn đó bằng
- A \(400 - 48\pi (c{m^2}).\)
- B \(400 - 96\pi (c{m^2}).\;\;\;\;\;\;\;\;\;\;\)
- C \(400 - 24\pi (c{m^2}).\)
- D \(400 - 36\pi (c{m^2}).\)
Phương pháp giải:
- Tính diện tích hình vuông.
- Tính diện tích mỗi nửa elip nhỏ, suy ra diện tích \(4\) phần bị khoét đi.
Công thức tính diện tích elip: \(S = \pi ab\).
Từ đó suy ra diện tích phần còn lại.
Lời giải chi tiết:
- Diện tích hình vuông \({S_1} = 20.20 = 400\left( {c{m^2}} \right)\).
- Diện tích mỗi nửa elip \({S_2} = \dfrac{1}{2}\pi ab = \dfrac{1}{2}.\pi .AB.\dfrac{{CD}}{2} = \dfrac{1}{2}\pi .6.\dfrac{8}{2} = 12\pi \left( {c{m^2}} \right)\).
\( \Rightarrow \) Diện tích phần bị khoét đi : \({S_3} = 4{S_2} = 4.12\pi = 48\pi \left( {c{m^2}} \right)\).
- Diện tích phần còn lại : \(S = {S_1} - {S_3} = 400 - 48\pi \left( {c{m^2}} \right)\)
Chọn A.













