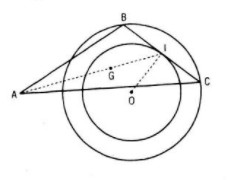
Câu 9 trang 35 SGK Hình học 11 Nâng caoCho đường tròn (O ; R) Đề bài Cho đường tròn (O ; R) và điểm A cố định. Một dây cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho →GA+→GB+→GC=→0 Quảng cáo  Lời giải chi tiết
Gọi I là trung điểm của BC thì OI⊥BC Ta có →GA+→GB+→GC=→0⇔→GA+2→GI=→0⇔→AG=23→AI Tức là phép vị tự V tâm A tỉ số 23 biến điểm I thành điểm G Trong tam giác vuông OIB ta có: OI=√OB2−IB2=√R2−(m2)2=R′ (không đổi) Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R) Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
