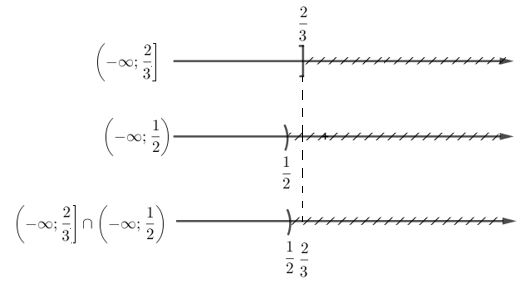
Bài 8 trang 50 SGK Đại số 10

LG a

$y =  {2 \over {x + 1}} + \sqrt {x + 3}$

Phương pháp giải:

+) Hàm số $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ xác định khi $g(x) \neq 0.$

+) Hàm số: $y = \sqrt {f\left( x \right)}$ xác định khi $f(x) \geq 0.$

Lời giải chi tiết:

$y =  {2 \over {x + 1}} + \sqrt {x + 3}$

Hàm số xác định $\Leftrightarrow \left\{ \begin{array}{l} x + 1 \ne 0\\ x + 3 \ge 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ne - 1\\ x \ge - 3 \end{array} \right..$

Tập xác định: $D = \left[ { - 3; + \infty } \right)\backslash \left\{ -1 \right\}$$= \left[ { - 3; - 1} \right) \cup \left( {-1; + \infty } \right).$

LG b

$y = \sqrt {2 - 3x}  - {1 \over {\sqrt {1 - 2x} }}$

Phương pháp giải:

+) Hàm số $y = \frac{{f\left( x \right)}}{{\sqrt {g\left( x \right)} }}$ xác định khi $g(x) > 0.$

+) Hàm số: $y = \sqrt {f\left( x \right)}$ xác định khi $f(x) \geq 0.$

Lời giải chi tiết:

$y = \sqrt {2 - 3x}  - {1 \over {\sqrt {1 - 2x} }}$ 

Hàm số xác định $\Leftrightarrow \left\{ \begin{array}{l} 2 - 3x \ge 0\\ 1 - 2x > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 3x \le 2\\ 2x < 1 \end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l} x \le \frac{2}{3}\\ x < \frac{1}{2} \end{array} \right. \Leftrightarrow x < \frac{1}{2}.$

Tập xác định: $D = \left( { - \infty ;\frac{1}{2}} \right).$

Chú ý:

Các em dùng trục số để lấy giao hai tập hợp như sau:

LG c

$y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.$

Phương pháp giải:

+) Hàm số $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ xác định khi $g(x) \neq 0.$

+) Hàm số: $y = \sqrt {f\left( x \right)}$ xác định khi $f(x) \geq 0.$

Lời giải chi tiết:

+ Xét trên $\left[ {1; + \infty } \right)$ thì $y = \frac{1}{{x + 3}}$

Hàm số xác định khi x + 3 ≠ 0 (luôn thỏa mãn với mọi x ≥ 1).

Vậy hàm số luôn xác định trên [1; +∞).

+ Xét trên (–∞; 1) thì $y = \sqrt {2 - x}$

Hàm số xác định khi 2 – x ≥ 0 ⇔ x ≤ 2 (luôn thỏa mãn với mọi x < 1).

Vậy hàm số luôn xác định trên (–∞; 1).

Kết luận: Hàm số xác định trên R.

Cách trình bày khác:

$y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.$ 

Hàm số xác định $\Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x \ge 1\\ x + 3 \ne 0 \end{array} \right.\\ \left\{ \begin{array}{l} x < 1\\ 2 - x \ge 0 \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x \ge 1\\ x \ne - 3 \end{array} \right.\\ \left\{ \begin{array}{l} x < 1\\ x \le 2 \end{array} \right. \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x \ge 1\\ x < 1 \end{array} \right..$

$\Leftrightarrow x\in R$.

Tập xác định: $D = R.$

HocTot.Nam.Name.Vn