Câu 7 trang 34 SGK Hình học 11 Nâng caoa. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A
Lựa chọn câu để xem lời giải nhanh hơn
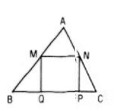
LG a Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số k=ABAM . Hãy dựng ảnh của hình vuông MNPQ qua phép vị tự V.
Lời giải chi tiết: Ta có →AB=k→AM và →AC=k→AN nên phép vị tự V biến điểm M thành điểm B, biến điểm N thành điểm C. Vậy V biến hình vuông MNPQ thành hình vuông BCP’Q’ như trên hình dưới:
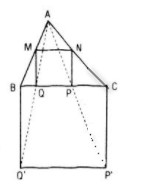
Quảng cáo  LG b Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC Lời giải chi tiết: Dựng hình vuông BCP’Q’ nằm ngoài tam giác ABC như hình
Lấy giao điểm P, Q của BC với các đoạn thẳng tương ứng AP’ và AQ’ Từ P và Q, kẻ các đường thẳng vuông góc với BC, lần lượt cắt AC và AB tại N và M Khi đó MNPQ chính là hình vuông cần dựng HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
