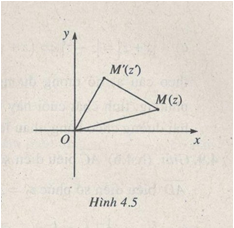
Câu 4.6 trang 177 sách bài tập Giải tích 12 Nâng cao

Đề bài

Gọi M, M’ theo thứ tự là các điểm của mặt phẳng phức biểu diễn số \(z \ne 0\)  và \(z' = {{1 + i} \over 2}z\). Chứng minh rằng tam giác OMM’ là tam giác vuông cân (O là gốc tọa độ)

Lời giải chi tiết

Ta có \(\left| {\overline {OM} } \right| = \left| z \right|,\)

\(\eqalign{& \left| {\overline {OM'} } \right| = \left| {{{1 + i} \over 2}} \right|\left| z \right| = {{\sqrt 2 } \over 2}\left| z \right|  \cr & \left| {\overline {MM'} } \right| = \left| {\overline {OM'}  - \overline {OM} } \right| = \left| {{{ - 1 + i} \over 2}} \right|\left| z \right| = {{\sqrt 2 } \over 2}\left| z \right| \cr} \)

Do \(\left| z \right| \ne 0,\) suy ra tam giác OMM’ là tam giác vuông cân đỉnh M’ (h.4.5)

HocTot.Nam.Name.Vn