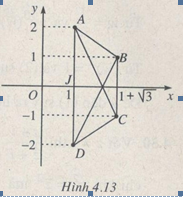
Câu 4.47 trang 184 sách bài tập Giải tích 12 Nâng cao

Đề bài

Cho A, B, C, D là bốn điểm trong mặt phẳng phức theo thứ tự biểu diễn các số

$1 + 2i$,         $1 + \sqrt 3  + i$,            $1 + \sqrt 3  - i$,        $1 - 2i$

Chứng minh rằng ABCD là một tứ giác nội tiếp đường tròn. Hỏi tâm đường tròn đó biểu diễn số phức nào ?

Lời giải chi tiết

Vì mỗi cặp số $1 + 2i$, $1 - 2i$ và $1 + \sqrt 3  + i$, $1 + \sqrt 3  - i$ là cặp số phức liên hợp nên hai điểm A, D, hai điểm B, C đối xứng qua $Ox$; phần thực của hai số đầu khác phần thực của hai số sau nên ABCD là một hình thang cân , do đó nó là một tứ giác nội tiếp đường tròn có tâm J nằm trên trục đối xứng $Ox$; J biểu diễn số thực $x$ sao cho $\left| {\overrightarrow {JA} } \right| = \overrightarrow {\left| {JB} \right|}  \Leftrightarrow \left| {1 - x + 2i} \right| = \left| {1 - x + \sqrt 3  + i} \right|$. Từ đó suy ra  $x$ = 1.

(Cách khác : $\overrightarrow {AB}$ biểu diễn số phức $\sqrt 3  - i$, $\overrightarrow {DB}$ biểu diễn số phức $\sqrt 3  + 3i$ mà ${{\sqrt 3  + 3i} \over {\sqrt 3  - i}} = \sqrt 3 i$ nên $\overrightarrow {AB} \overrightarrow {.DB}  = 0$. Tương tự (hay vì lí do đối xứng qua $Ox$), $\overrightarrow {DC} .\overrightarrow {AC}  = 0$. Từ đó suy ra AD là một đường kính của đường tròn đi qua A, B, C, D . ( h.4.13)

HocTot.Nam.Name.Vn