Câu 3 trang 34 SGK Hình học 11 Nâng cao .Cho đường thẳng d đi qua hai điểm phân biệt P, Q Đề bài Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) và AM + BN bé nhất Lời giải chi tiết
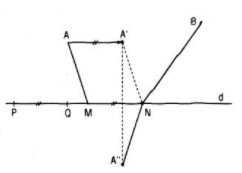
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \overrightarrow {PQ} \) thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N Ta có: AM + BN = A’N + BN Gọi A” là điểm đối xứng của A’ qua d, khi đó: A’N + BN = A”N + BN ≥ A”B Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d Từ đó tìm được điểm M thỏa \(\overrightarrow {MN} = \overrightarrow {AA'} = \overrightarrow {PQ} \) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
