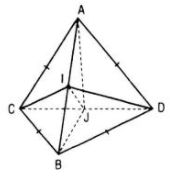
Câu 27 trang 112 SGK Hình học 11 Nâng cao

Đề bài

Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD.

a. Tính AB, IJ theo a và x.

b. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc ?

Quảng cáo

Lời giải chi tiết

a. Vì J là trung điểm của CD và AC = AD nên AJ ⊥ CD.

Do mp(ACD) ⊥ mp(BCD) nên AJ ⊥ mp(BCD)

Mặt khác, AC = AD = BC = BD nên tam giác AJB vuông cân, suy ra $AB = AJ\sqrt 2 ,A{J^2} = {a^2} - {x^2}$ $hay\,AJ = \sqrt {{a^2} - {x^2}} .$

Vậy $AB = \sqrt {2\left( {{a^2} - {x^2}} \right)}$ với a > x

Do IA = IB, tam giác AJB vuông tại J nên $JI = {1 \over 2}AB,$ tức là $IJ = {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} .$

b) 

+Tam giác ABC có AC = BC

nên tam giác ABC cân tại C,

có CI là đường trung tuyến nên đồng thời là đường cao:

CI ⊥ AB (3)

Tam giác ABD cân tại D có DI là đường trung tuyến nên

DI ⊥ AB (4)

Hai mp (ABC) và (ABD) cắt nhau theo giao tuyến là AB (5)

Từ (3) , (4) và (5) suy ra góc giữa hai mp(ABC) và (ABD) là góc CID.

Vậy mp(ABC) ⊥ mp(ABD) $\Leftrightarrow \widehat {CID} = 90^\circ$

$\Leftrightarrow IJ = {1 \over 2}CD$ $\Leftrightarrow {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)}  = {1 \over 2}.2x$ $\Leftrightarrow 2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2}$

$\Leftrightarrow x = {{a\sqrt 3 } \over 3}$

HocTot.Nam.Name.Vn