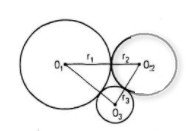
Câu 23 trang 23 SGK Hình học 11 Nâng cao

Đề bài

Hình H₁ gồm ba đường tròn \(\left( {{O_1};{r_1}} \right),\left( {{O_2};{r_2}} \right)\) và \(\left( {{O_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Hình H₂ gồm ba đường tròn \(\left( {{I_1};{r_1}} \right),\left( {{I_2};{r_2}} \right)\) và \(\left( {{I_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H₁ và H₂ bằng nhau.

Lời giải chi tiết

Ta có

\({{O_1}{O_2} = {r_1} + {\rm{ }}{r_2} = {I_1}{I_2}}\)
\({{O_2}{O_3} = {r_2} + {\rm{ }}{r_3} = {I_2}{I_3}} \)
\({{O_3}{O_1} = {r_3} + {\rm{ }}{r_1} = {I_3}{I_1}} \)

Suy ra \(\Delta {O_1}{O_2}{O_3} = \Delta {I_1}{I_2}{I_3}\) nên có phép dời hình F biến ba điểm O₁, O₂, O₃ lần lượt thành ba điểm I₁, I₂, I₃

Hiển nhiên khi đó F biến ba đường tròn \(({O_{1}}{\rm{; }}{r_1}),{\rm{ }}({O_2};{\rm{ }}{r_2}),{\rm{ }}({O_3};{\rm{ }}{r_3})\) lần lượt thành ba đường tròn \(({I_1};{r_1}),({I_2};{r_2}),({I_3};{r_3})\), tức là biến hình H₁ thành hình H₂

Vậy hai hình H₁ và H₂ bằng nhau

HocTot.Nam.Name.Vn