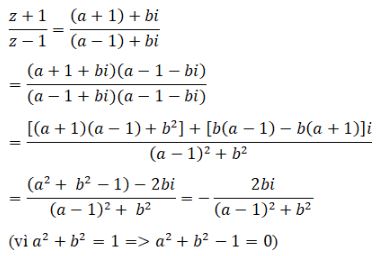Câu 19 trang 214 SGK Giải tích 12 Nâng cao

LG a

Xác định phần thực của số phức \({{z + 1} \over {z - 1}}\) biết rằng |z| = 1 và z ≠ 1

Phương pháp giải:

Xét \(w={{z + 1} \over {z - 1}}\). Sử dụng tính chất: \(w + \overline w  = 2a\) để suy ra phần thực của w.

Lời giải chi tiết:

Ta có:

\(|z| = 1 \Rightarrow z.\overline z  = 1 \Rightarrow \overline z  = {1 \over z}\)

Với \(z ≠ 1\)

Xét \(w={{z + 1} \over {z - 1}}\) ta có:

\(\eqalign{
& w+\overline w={{z + 1} \over {z - 1}} + \overline {({{z + 1} \over {z - 1}})}\cr & = {{z + 1} \over {z - 1}} + {{\overline z + 1} \over {\overline z - 1}} \cr 
& = {{z + 1} \over {z - 1}} + {{{1 \over z} + 1} \over {{1 \over z} - 1}} \cr &= {{z + 1} \over {z - 1}} + {{1 + z} \over {1 - z}} = 0 \cr} \)

Suy ra: \({{z + 1} \over {z - 1}}\) là số ảo nên có phần thực bằng 0.

Cách khác:

Giả sử z=a+bi với a²+b²=1 và a+bi ≠ 1.

Suy ra: \({{z + 1} \over {z - 1}}\) là số ảo nên có phần thực bằng 0.

LG b

Chứng minh rằng nếu \({{z + 1} \over {z - 1}}\) là số ảo thì |z| = 1.

Phương pháp giải:

Sử dụng tính chất: Nếu w là số ảo thì \(w + \overline w  = 0\) hay \(w =- \overline w  \)

Lời giải chi tiết:

Xét \(w={{z + 1} \over {z - 1}}\).

Nếu \({{z + 1} \over {z - 1}}\) là số ảo thì

\(w =  - \overline w  \Leftrightarrow \frac{{z + 1}}{{z - 1}} =  - \overline {\left( {\frac{{z + 1}}{{z - 1}}} \right)} \)

\(\eqalign{
& \Leftrightarrow  {{z + 1} \over {z - 1}} = - {{\overline z + 1} \over {\overline z - 1}} \cr 
& \Rightarrow (z + 1)(\overline z - 1) = (\overline z + 1)(1 - z) \cr 
& \Leftrightarrow z.\overline z  + \overline z  - z - 1 = \overline z  + 1 - z.\overline z  - z\cr & \Leftrightarrow 2z\overline z  = 2\cr &\Leftrightarrow  z.\overline z = 1 \cr} \)

\( \Rightarrow \left| z \right|.\left| {\overline z } \right| = 1 \Leftrightarrow {\left| z \right|^2} = 1 \Leftrightarrow \left| z \right| = 1\)

Vậy |z| = 1.

Cách khác:

Theo câu a, ta có: \(\frac{{z - 1}}{{z + 1}} = \frac{{{a^2} + {b^2} - 1}}{{{{\left( {a - 1} \right)}^2} + {b^2}}} - \frac{{2b}}{{{{\left( {a - 1} \right)}^2} + {b^2}}}i\)

Nên (z+1)/(z-1) là số ảo thì a²+b²-1=0 <=> a²+b²=1 <=> |z| = 1 (đpcm)

 HocTot.Nam.Name.Vn