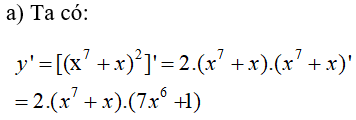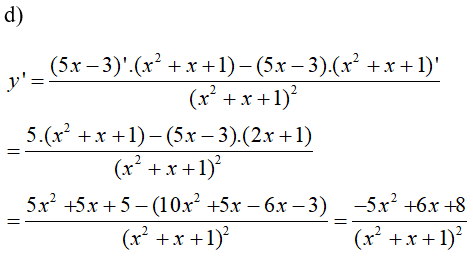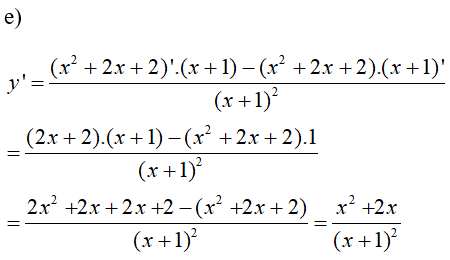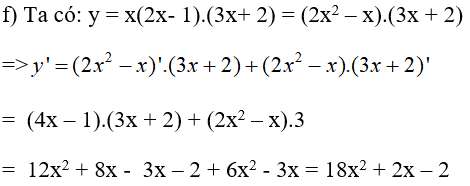Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao

LG a

 \(y = \left( {{x^7} + {x}} \right)^2\)

Phương pháp giải:

Khai triển hằng đẳng thức và tính đạo hàm.

Lời giải chi tiết:

Ta có: \(y = {x^{14}} + 2{x^8} + {x^2} \) \(\Rightarrow y' = 14{x^{13}} + 16{x^7} + 2x\).

Cách khác:

LG b

\(y = \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)\)

Phương pháp giải:

Sử dụng công thức đạo hàm của tích (uv)'=u'v+uv'

Lời giải chi tiết:

\(\eqalign{  & y' = \left( {{x^2} + 1} \right)'\left( {5 - 3{x^2}} \right) + \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)'  \cr  &  = 2x\left( {5 - 3{x^2}} \right) - 6x\left( {{x^2} + 1} \right) \cr & = 10x - 6{x^3} - 6{x^3} - 6x\cr &= 4x - 12{x^3} \cr} \)

LG c

\(y = {{2x} \over {{x^2} - 1}}\)

Phương pháp giải:

Đạo hàm của thương \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)

Lời giải chi tiết:

\(y' \) \( = \frac{{\left( {2x} \right)'\left( {{x^2} - 1} \right) - 2x\left( {{x^2} - 1} \right)'}}{{{{\left( {{x^2} - 1} \right)}^2}}}\)  \(= {{2\left( {{x^2} - 1} \right) - 2x\left( {2x} \right)} \over {{{\left( {{x^2} - 1} \right)}^2}}} \) \( = \frac{{ - 2{x^2} - 2}}{{{{\left( {{x^2} - 1} \right)}^2}}}\) \(= {{ - 2\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} - 1} \right)}^2}}}\)

LG d

\(y = {{5x - 3} \over {{x^2} + x + 1}}\)

Lời giải chi tiết:

\(y' = {{ - 5{x^2} + 6x + 8} \over {{{\left( {{x^2} + x + 1} \right)}^2}}}\)

LG e

 \(y = {{{x^2} + 2x + 2} \over {x + 1}}\)

Lời giải chi tiết:

\(y'  = {{{x^2} + 2x} \over {{{\left( {x + 1} \right)}^2}}}\)

LG f

 \(y = x\left( {2x - 1} \right)\left( {3x + 2} \right)\)

Lời giải chi tiết:

\(\eqalign{  & y = 18{x^2} + 2x - 2 \cr} \)

HocTot.Nam.Name.Vn