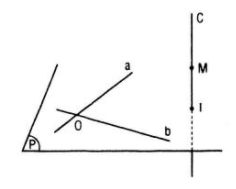
Câu 10 trang 50 SGK Hình học 11 Nâng caoCho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định Đề bài Cho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định. Quảng cáo  Lời giải chi tiết
Ta có: {M∈(M,a)M∈(M,b) ⇒M∈(M,a)∩(M,b) Vì O=a∩b ⇒{O∈a⊂(M,a)O∈b⊂(M,b) nên O∈(M,a)∩(M,b) ⇒(M,a)∩(M,b)=MO Vì M ∈ c nên MO ⊂ mp(O, c) Vậy giao tuyến của hai mặt phẳng (M, a), (M, b) nằm trên mặt phẳng (O, c) cố định. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
