Nội dung từ Loigiaihay.Com
Cách tính thể tích vật thể ứng dụng tích phân - Toán 12
1. Khái niệm tích phân
2. Công thức tính thể tích vật thể ứng dụng tích phân
3. Bài tập vận dụng
1. Khái niệm tích phân
Cho hàm số f(x) liên tục trên đoạn [a;b]. Nếu F(x) là một nguyên hàm của f(x) trên đoạn [a;b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x).
.
Trong đó:
+ là dấu tích phân.
+ a và b là cận tích phân (a là cận dưới, b là cận trên).
+ f(x)dx là biểu thức dưới dấu tích phân.
+ f(x) là hàm số dưới dấu tích phân.
Lưu ý:
+ ;
+ ;
2. Công thức tính thể tích vật thể ứng dụng tích phân
Cho một vật thể trong không gian Oxyz. Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm x thì phần chung giữa mặt phẳng và vật thể có diện tích S(x). Giả sử S(x) là hàm số liên tục trên đoạn . Khi đó thể tích V của vật thể B được tính bởi công thức
Ví dụ minh hoạ:
Hãy sử dụng tích phân tính thể tích khối lăng trụ có diện tích đáy bằng S (không đổi) và chiều cao h.
Giải:
Chọn trục Ox song song với đường cao của khối lăng trụ, hai đáy nằm trong mặt phẳng vuông góc với Ox tại x = 0, x = h.
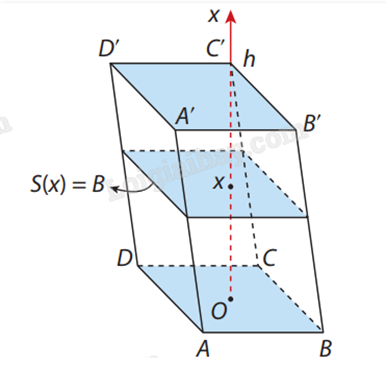
Khi cắt khối lăng trụ bởi mặt phẳng vuông góc với trục Ox tại điểm x , thì phần chung giữa mặt phẳng và khối lăng trụ là một hình phẳng có diện tích không đổi.
Thể tích khối lăng trụ là:
(đvdt).
3. Bài tập vận dụng
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống

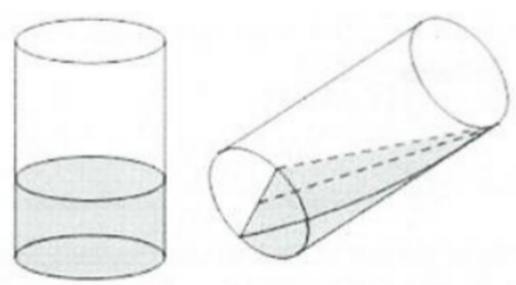
Bạn Nam có một ống thủy tinh hình trụ, đường kính trong lòng đáy cốc là 10 cm, chiều cao cốc là 15 cm đang đựng nước. Khi bạn Nam nghiêng cốc nước thì thấy mặt nước đi qua đường kính đáy và chạm miệng cốc. Thể tích lượng nước trong cốc là bao nhiêu ?
Các bài khác cùng chuyên mục
- Cách tính thể tích khối tròn xoay ứng dụng tích phân - Toán 12
- Phương trình tổng quát của mặt phẳng - Toán 12
- Cách xác định vecto pháp tuyến của mặt phẳng - Toán 12
- Cách xác định vecto pháp tuyến từ cặp vecto chỉ phương của mặt phẳng - Toán 12
- Cách xác định điểm thuộc và không thuộc mặt phẳng - Toán 12













