Nội dung từ Loigiaihay.Com
Cách tìm m để hàm số đồng biến, nghịch biến ứng dụng đạo hàm - Toán 12
1. Hàm số đồng biến, nghịch biến là gì?
2. Cách tìm m để hàm số đồng biến hoặc nghịch biến trên tập xác định
3. Cách tìm m để hàm số đồng biến hoặc nghịch biến trên khoảng cho trước
4. Bài tập vận dụng
1. Hàm số đồng biến, nghịch biến là gì?
Giả sử hàm số y=f(x) xác định trên K.
Hàm số y=f(x) gọi là đồng biến (tăng) trên K nếu với mọi x1, x2 thuộc K mà x1<x2 thì f(x1)<f(x2).
Hàm số y=f(x) gọi là nghịch biến (giảm) trên K nếu với mọi x1, x2 thuộc K mà x1<x2 thì f(x1)>f(x2).
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
2. Cách tìm m để hàm số đồng biến hoặc nghịch biến trên tập xác định
Cho hàm số y = f(x).
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính đạo hàm y’ = f’(x).
Bước 3:
- Đề bài yêu cầu hàm số đồng biến thì tìm điều kiện để:
+ f′(x)≥m với hàm đa thức.
+ f′(x)>m với hàm phân thức bậc nhất.
- Đề bài yêu cầu hàm số nghịch biến thì tìm điều kiện để:
+ f′(x)≤m với hàm đa thức.
+ f′(x)<m với hàm phân thức bậc nhất.
Dấu “=” xảy ra tại hữu hạn điểm.
Ví dụ minh hoạ:
a) Tìm tất cả các giá trị của m để hàm số y=x3+(m+1)x2+3x+2025 đồng biến trên R.
b) Tìm tất cả các giá trị m để hàm số y=m2−4m(x+m)2 nghịch biến trên các khoảng xác định.
Giải:
a) y=x3+(m+1)x2+3x+2025.
TXĐ: D=R.
Ta có y′=3x2+2(m+1)x+3.
Hàm số y=x3+(m+1)x2+3x+2025 đồng biến trên R khi và chỉ khi y′≥0, ∀x∈R.
Khi đó 3x2+2(m+1)x+3≥0⇔{Δ′=(m+1)2−9≤0a=3>0⇔m2+2m−8≤0⇔−4≤m≤2.
b) y=mx+4mx+m.
TXĐ: D=R∖{−m}.
Ta có y′=m2−4m(x+m)2.
Hàm số y=mx+4mx+m nghịch biến trên khoảng xác định khi và chỉ khi:
y′=m2−4m(x+m)2<0⇔m2−4m<0⇔0<m<4.
3. Cách tìm m để hàm số đồng biến hoặc nghịch biến trên khoảng cho trước
1) Đối với hàm đa thức:
Bước 1: Tính đạo hàm f’(x).
Bước 2: Để hàm số đồng biến trên (p;q), tìm m để f′(x)≥0 ∀x∈(p;q). Để hàm số nghịch biến trên (p;q), tìm m để f′(x)≤0 ∀x∈(p;q).
Cách 2: Cô lập m và xét dấu theo quy tắc:
+ m≥f(x),∀x∈(p;q)⇔m≥max(p;q)f(x).
+ m≤f(x),∀x∈(p;q)⇔m≤max(p;q)f(x).
2) Đối với hàm phân thức bậc nhất trên bậc nhất y=ax+bcx+d:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính đạo hàm f’(x).
Bước 3: Kết luận:
- Hàm số đồng biến trên khoảng (p;q) ⇔{f′(x)>0−dc∉(p;q).
- Hàm số nghịch biến trên khoảng (p;q) ⇔{f′(x)<0−dc∉(p;q).
Ví dụ minh hoạ:
a) Tìm tất cả các giá trị thực của tham số m để hàm số y=x3−3x2+(1−m)x đồng biến trên (2;+∞).
b) Tìm tất cả các giá trị thực của tham số m để hàm số y=x+3x+m đồng biến trên (−∞;−6).
Giải:
a) Xét f(x)=x3−3x2+(1−m)x trên (2;+∞).
Tập xác định: D=R.
Ta có f′(x)=3x2−6x+(1−m).
Để f(x) đồng biến trên (2;+∞) thì f′(x)≥0,∀x∈(2;+∞)
⇔3x2−6x+(1−m)≥0,∀x∈(2;+∞)
⇔3x2−6x+1≥m,∀x∈(2;+∞)
⇔m≤min(2;+∞)(3x2−6x+1).
Đặt g(x)=3x2−6x+1; g′(x)=6x−6=0⇔x=1.
Ta có bảng biến thiên:
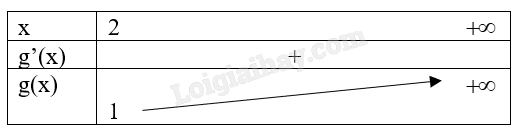
Vậy m≤min(2;+∞)(3x2−6x+1)⇔m≤1.
b) Xét f(x)=x+3x+m trên (−∞;−6).
Tập xác định: D=R∖{−m}.
Để hàm số f(x)=x+3x+m đồng biến trên (−∞;−6), ta có:
⇔{f′(x)>0−m∉(−∞;−6)⇔{m−3>0−m≥−6⇔{m>3m≤6⇔3<m≤6.
4. Bài tập vận dụng
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \dfrac{{mx + 2}}{{2x + m}}$ nghịch biến trên từng khoảng xác định của nó?
Các bài khác cùng chuyên mục
- Cách tìm số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối - Toán 12
- Cách tìm số điểm cực trị của hàm số dựa vào hàm f'(x) - Toán 12
- Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số dựa vào bảng biến thiên - Toán 12
- Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số dựa vào đồ thị - Toán 12
- Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số dựa vào công thức hàm số - Toán 12













