Nội dung từ Loigiaihay.Com
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng
Từ đó có hệ thức cần chứng minh.
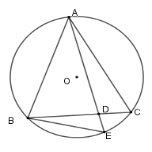
Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) )
Xét \(\Delta ABD\) và \(\Delta AEB\) có \(\widehat A\) chung và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD\)
Đáp án : A

Các bài tập cùng chuyên đề
Hình nào dưới đây biểu diễn góc nội tiếp?

Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
Khẳng định nào sau đây là sai?
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
Tam giác $ABC$ nằm trên đường tròn $\left( {O;R} \right)$ biết góc $\widehat C = {45^o}$ và $AB = a$. Bán kính đường tròn $\left( O \right)$ là












