Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác $ABC$ vuông tại $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$AC \approx 4,39 (cm);BC \approx 6,66 (cm)$
-
B.
$AC \approx 4,38(cm);BC \approx 6,64(cm)$
-
C.
$AC \approx 4,38(cm);BC \approx 6,67(cm)$
-
D.
$AC \approx 4,37(cm);BC \approx 6,67(cm)$
Phương pháp giải
Sử dụng tỉ số lương giác của góc nhọn, định lý Pytago để tính cạnh.
Lời giải của GV HocTot.Nam.Name.Vn
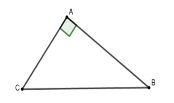
Vì tam giác $ABC$ vuông tại $A$ nên $\cot C = \dfrac{{AC}}{{AB}} \Rightarrow AC = AB.\cot C = 5.\dfrac{7}{8} = \dfrac{{35}}{8} \approx 4,38\,\,cm$
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{35}}{8}} \right)^2} \Rightarrow BC \approx 6,64\)
Vậy $AC \approx 4,38(cm);BC \approx 6,64(cm)$.
Đáp án : B
Các bài tập cùng chuyên đề
Bài 1 :
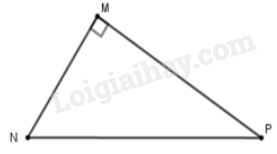
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
Xem lời giải >>
Bài 2 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
Xem lời giải >>
Bài 3 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
Xem lời giải >>
Bài 4 :
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng?
Xem lời giải >>
Bài 5 :
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
Xem lời giải >>
Bài 6 :
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
Xem lời giải >>
Bài 7 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
Xem lời giải >>
Bài 8 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
Xem lời giải >>
Bài 9 :
Cho tam giác $ABC$ vuông tại $A$. Hãy tính $\tan C$ biết rằng \(\cot B = 2\).
Xem lời giải >>
Bài 10 :
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
Xem lời giải >>
Bài 11 :
Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)
Xem lời giải >>
Bài 12 :
Sắp xếp các tỉ số lượng giác \(\tan 43^\circ ,\,\,\cot 71^\circ ,\,\,\tan 38^\circ ,\,\,\cot 69^\circ 15',\,\tan 28^\circ \) theo thứ tự tăng dần.
Xem lời giải >>
Bài 13 :
Tính giá trị biểu thức $A = {\sin ^2}1^\circ + {\sin ^2}2^\circ + ... + {\sin ^2}88^\circ + {\sin ^2}89^\circ + {\sin ^2}90^\circ $
Xem lời giải >>
Bài 14 :
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
Xem lời giải >>
Bài 15 :
Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
Xem lời giải >>
Bài 16 :
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
Xem lời giải >>
Bài 17 :
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
Xem lời giải >>
Bài 18 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
Xem lời giải >>
Bài 19 :
Cho $ \alpha $ là góc nhọn. Tính \(\cot \alpha \) biết \(\sin \alpha = \dfrac{5}{{13}}\).
Xem lời giải >>
Bài 20 :
Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $
Xem lời giải >>