Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
-
A.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 8,52\)
-
B.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 4,42\)
-
C.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 4,24\)
-
D.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 3,97\)
Phương pháp giải
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng tính chất tam giác cân.
Sử dụng định lý tổng ba góc trong một tam giác.
Lời giải của GV HocTot.Nam.Name.Vn
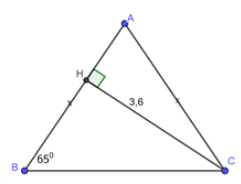
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\)
Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác)
\( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\)
Xét \(\Delta ACH\) vuông tại \(H\) ta có:
\(\sin A = \dfrac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \dfrac{{3,6}}{{AC}}\)\( \Rightarrow AC = \dfrac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\)
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\)
Xét \(\Delta BCH\) vuông tại \(H\) ta có:
\(\sin B = \dfrac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \dfrac{{3,6}}{{BC}} \)\(\Rightarrow BC = \dfrac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\)
Đáp án : D
Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng?
Xem lời giải >>
Bài 2 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai?
Xem lời giải >>
Bài 3 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$
Xem lời giải >>
Bài 4 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm,\widehat B = 40^\circ .\) Tính $AC;\widehat C$ . (làm tròn đến chữ số thập phân thứ hai)
Xem lời giải >>
Bài 5 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\) . Tính $AC;\widehat B$ .
Xem lời giải >>
Bài 6 :
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
Xem lời giải >>
Bài 7 :
Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?
Xem lời giải >>
Bài 8 :
Cho tứ giác $ABCD$ có $\widehat A = \widehat D = {90^0},\widehat C = {40^0},AB = 4cm,AD = 3cm.$ Tính diện tích tứ giác $ABCD.$ (làm tròn đến chữ số thập phân thứ hai)
Xem lời giải >>
Bài 9 :
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\)
Xem lời giải >>
Bài 10 :
Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
Xem lời giải >>
Bài 11 :
Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\).
Tính \(DA;DC\) theo \(a\).
Xem lời giải >>
Bài 12 :
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
Xem lời giải >>
Bài 13 :
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\).
Xem lời giải >>