Nội dung từ Loigiaihay.Com
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.
-
A.
\(PQ\) luôn tiếp xúc với một đường tròn cố định
-
B.
\(PQ\) không tiếp xúc với một đường tròn cố định nào
-
C.
\(PQ = a\)
-
D.
\(PQ = OP\)
Sử dụng tính chất tia phân giác, hai tam giác bằng nhau
Và điều kiện tiếp xúc của đường thẳng với đường tròn.
Đường thẳng \(d\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(M\) khi \(M \in \left( O \right)\) và \(OM = R.\)
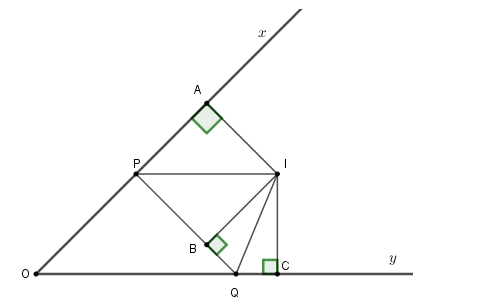
Gọi I là giao điểm các tia phân giác của \(\widehat {xPQ};\,\widehat {yQP}\) và A, B, C lần lượt là hình chiếu của I lên Ox, PQ và Oy.
Vì I thuộc phân giác của góc xPQ nên IA = IB.
Xét ∆PAI và ∆PBI có :
+ IA = IB (cmt)
+ Chung PI
+ \(\widehat {PAI} = \widehat {PBI} = 90^\circ \)
nên ∆PAI = ∆PBI (cạnh huyền – cạnh góc vuông) ,
Suy ra PA = PB.
Lí luận tương tự, ta có \(QB = QC.\)
\(OA + OC = OP + PA + OQ + QC\) \( = OP + PB + OQ + QB = OP + PQ + QO = 2a\) (do chu vi ∆OPQ bằng 2a).
Vì IA = IB và IB = IC (cmt) nên IA = IC.
Xét ∆OAI và ∆OCI có
+ IA = IC (cmt)
+ \(\widehat {OAI} = \widehat {OCI} = 90^\circ \)
+ cạnh chung OI
nên ∆OAI = ∆OCI (cạnh huyền – cạnh góc vuông) \( \Rightarrow OA = OC = \dfrac{{2a}}{2} = a{\rm{ }}.\)
Vì a không đổi và A, C thuộc tia Ox, Oy cố định nên A và C cố định.
Do A và C lần lượt là hình chiếu của I lên Ox, Oy nên hai đường thẳng AI và CI cố định hay I cố định.
Do I và A cố định nên độ dài đoạn thẳng AI không đổi.
Do IA = IB (cmt) nên IB là bán kính của đường tròn (I ; IA), mà IB ⊥ PQ tại B nên PQ tiếp xúc với đường tròn (I; IA) cố định.
Đáp án : A

Các bài tập cùng chuyên đề
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.












