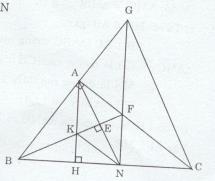
Bài tập 4 trang 130 Tài liệu dạy – học Toán 7 tập 2 - Hình học

Đề bài

Tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ $BE \bot AN\,\,\left( {E \in AN} \right)$

a) Chứng minh BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh tam giác GBC cân.

Lời giải chi tiết

a) BA = BN => ∆ABN cân tại B.

Mà BE là đường cao của ∆ABN (vì $BE \bot AN$ tại E)

Nên BE cũng là đường phân giác của ∆ABN

Vậy BE là tia phân giác của $\widehat {ABN}.$

b) ∆ABN có hai đường cao BE và AH cắt nhau tại K (gt).

=> K là trực tâm của ∆ABN

=> NK là đường cao của ∆ABN

$\Rightarrow NK \bot AB$

Mà $CA \bot AB$ (∆ABC vuông tại A)

Nên NK // CA.

c) Ta có: $\widehat {NFC} = \widehat {FNK}$ (hai góc so le trong và NK // AC)

$\widehat {NFC} = \widehat {AFG}$ (đối đỉnh)

$\Rightarrow \widehat {FNK} = \widehat {AFG}$

Mà $\widehat {FNK}$ và $\widehat {AFG}$ ở vị trí đồng vị. Nên AH // GN

Lại có $AH \bot BC$ (AH là đường cao của ∆ABC) $\Rightarrow GN \bot BC.$

Xét ∆ABC và ∆GNB ta có $\widehat {BAC} = \widehat {BNG}( = 90^\circ )$

AB = BN (gt)

$\widehat {ABC}$ chung

Do đó: ∆ABC = ∆NBG (g.c.g) => BC = BG

Vậy ∆BGC cân tại B.

HocTot.Nam.Name.Vn