Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) cân tại A, trung tuyến AM. Gọi I là trung điểm của AC. Trên tia MI lấy điểm N sao cho I là trung điểm của MN.
a) Tứ giác AMCN là hình gì? Vì sao?
b) Gọi E là trung điểm của AM. Chứng minh E là trung điểm của BN.
c) Gọi K là trung điểm của AB. Tìm điều kiện để AKMI là hình vuông.
a) Dựa vào I là trung điểm của AC, I là trung điểm của M và tam giác ABC cân tại A có AM là trung tuyến để xác định AMCN là hình gì.
b) Chứng minh ABMN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
c) Xác định xem AKMI là hình gì. Tìm thêm điều kiện để AKMI là hình vuông.
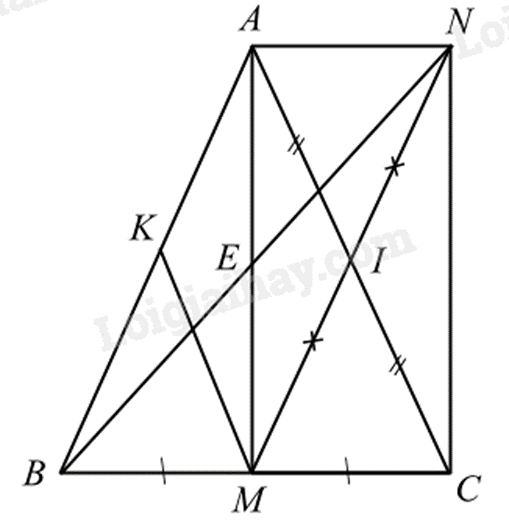
a) Xét tứ giác AMCN có:
IA = IC (I là trung điểm của AC)
IM = IN (I là trung điểm của MN)
Suy ra tứ giác AMCN là hình bình hành.
Xét tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao nên \(AM \bot BC\) hay \(\widehat {AMC} = 90^\circ \).
Hình bình hành AMCN có \(\widehat {AMC} = 90^\circ \) nên AMCN là hình chữ nhật.
b) Vì tứ giác AMCN là hình chữ nhật nên AN // MC hay AN // BM và AN = CM.
Do đó AN = BM (cùng bằng CM)
Xét tứ giác ABMN có:
AN = BM (cmt)
AN // BM (cmt)
suy ra ABMN là hình bình hành.
Nên hai đường chéo AM và BN cắt nhau tại trung điểm của mỗi đường.
Mà E là trung điểm của AM nên E cũng là trung điểm của BN.
c) Xét tam giác ABC có:
M là trung điểm của BC (AM là đường trung tuyến)
I là trung điểm của AC
nên MI là đường trung bình của tam giác ABC, suy ra MI // AB và MI = \(\frac{1}{2}\)AB.
Mà K là trung điểm của AB nên AK = \(\frac{1}{2}\)AB.
Do đó MI // AK và MI = AK (= \(\frac{1}{2}\)AB)
Xét tứ giác AKMI có MI // AK và MI = AK nên AKMI là hình bình hành.
Mà AI = MI (vì AMCN là hình chữ nhật)
Do đó AKMI là hình thoi.
Để AKMI là hình vuông thì hình thoi AKMI cần có thêm góc vuông ở đỉnh.
Khi đó \(\widehat {KAI} = 90^\circ \) hay tam giác ABC vuông tại A.
Mà tam giác ABC cân tại A.
Vậy để AKMI là hình vuông thì ta cần thêm điều kiện tam giác ABC vuông cân tại A.

Các bài tập cùng chuyên đề
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh \(MI = IK = KN\).
Cho hình bình hành ABCD, AC cắt BD tại O. Đường phân giác góc A cắt BD tại M, đường phân giác góc D cắt AC tại N. Chứng minh MN//AD.
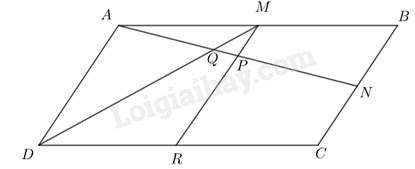
Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
a) \(MP\parallel AD,\,\,MP = \frac{1}{4}AD\)
b) \(AQ = \frac{2}{5}AN\)
c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và \(PR = \frac{3}{4}AD\).
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
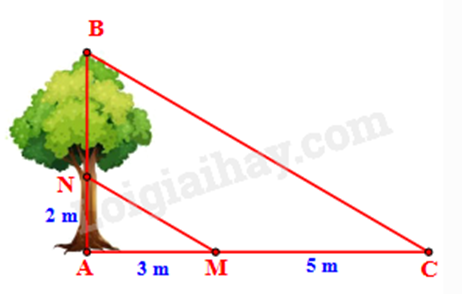
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.