Nội dung từ Loigiaihay.Com
Công thức \(\log x = 11,8 + 1,5M\) cho biết mối liên hệ giữa năng lượng x tạo ra (tính theo erg, 1erg tương đương với \({10^{ - 7}}\)jun) với độ lớn M theo thang Richter của một trận động đất.
a) Trận động đất có độ lớn 5 độ Richter tạo ra năng lượng gấp bao nhiêu lần so với trận động đất có độ lớn 3 độ Richter?
b) Người ta ước lượng rằng một trận động đất có độ lớn khoảng từ 4 đến 6 độ Richter. Năng lượng do trận động đất đó tạo ra nằm trong khoảng nào?
a) Sử dụng kiến thức về phép tính lôgarit để tính: Với \(a > 0,a \ne 1,M > 0,N > 0\) ta có: \({\log _a}\frac{M}{N} = {\log _a}M - {\log _a}N\)
b) Sử dụng kiến thức về giải bất phương trình lôgarit để giải bất phương trình:
Bảng tổng kết về nghiệm của các bất phương trình:
|
Bất phương trình |
\(a > 1\) |
\(0 < a < 1\) |
|
\({\log _a}x > b\) |
\(x > {a^b}\) |
\(0 < x < {a^b}\) |
|
\({\log _a}x \ge b\) |
\(x \ge {a^b}\) |
\(0 < x \le {a^b}\) |
|
\({\log _a}x < b\) |
\(0 < x < {a^b}\) |
\(x > {a^b}\) |
|
\({\log _a}x \le b\) |
\(0 < x \le {a^b}\) |
\(x \ge {a^b}\) |
Chú ý:
+ Nếu \(a > 1\) thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}v\left( x \right) > 0\\u\left( x \right) > v\left( x \right)\end{array} \right.\)
+ Nếu \(0 < a < 1\) thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\)
a) Gọi \({x_1},{x_2}\) (erg) lần lượt là năng lượng tạo ra của hai trận động đất có độ lớn lần lượt là \({M_1} = 5,{M_2} = 3\) (độ Richter)
Ta có: \(\log {x_1} = 11,8 + 1,5{M_1};\log {x_2} = 11,8 + 1,5{M_2}\)
Do đó, \(\log {x_1} - \log {x_2} = 1,5\left( {{M_1} - {M_2}} \right) \Rightarrow \log \frac{{{x_1}}}{{{x_2}}} = 3 \) \( \Leftrightarrow \frac{{{x_1}}}{{{x_2}}} = {10^3} = 1000\)
Vậy trận động đất có độ lớn 5 độ Richter tạo ra năng lượng gấp 1000 lần so với trận động đất có độ lớn 3 độ Richter.
b) Theo đầu bài ta có:
\(11,8 + 1,5.4 \le \log x \le 11,8 + 1,5.6 \) \( \Leftrightarrow 17,8 \le \log x \le 20,8 \) \( \Leftrightarrow {10^{17,8}} \le x \le {10^{20,8}}\)

Các bài tập cùng chuyên đề
Giải các bất phương trình sau:
a) \(0,{1^{2x - 1}} \le 0,{1^{2 - x}};\)
b) \({3.2^{x + 1}} \le 1.\)
Áp suất khí quyển p (tính bằng kilopascal, viết tắt là kPa) ở độ cao h (so với mực nước biển, tính bằng km) được tính theo công thức sau:
\(\ln \left( {\frac{p}{{100}}} \right) = - \frac{h}{7}.\)
(Theo britannica.com)
a) Tính áp suất khí quyển ở độ cao 4 km.
b) Ở độ cao trên 10 km thì áp suất khí quyển sẽ như thế nào?
Giải các bất phương trình sau:
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right);\)
b) \(2\log \left( {2x + 1} \right) > 3.\)
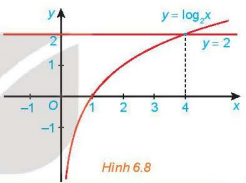
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)
Nước uống đạt tiêu chuẩn phải có độ pH nằm trong khoảng từ 6,5 đến 8,5 (theo Quy chuẩn Việt Nam QCVN 01:2009/BYT). Nồng độ H+ trong nước uống tiêu chuẩn phải nằm trong khoảng nào?
Giải các bất phương trình sau:
a) \({\log _{\frac{1}{3}}}\left( {x + 1} \right) < 2\);
b) \({\log _5}\left( {x + 2} \right) \le 1\).
Biết rằng máu của người bình thường có độ pH từ 7,30 đến 7,45 (nguồn: Hoá học 11, NXB Giáo dục Việt Nam, năm 2017, trang 15). Nồng độ H+ trong máu nhận giá trị trong miền nào?
Giải các bất phương trình sau:
a) \({\log _2}\left( {x - 2} \right) < 2\);
b) \(\log \left( {x + 1} \right) \ge \log \left( {2x - 1} \right)\).
Số nguyên \(x\) nhỏ nhất thoả mãn \({\log _{0,1}}\left( {1 - 2x} \right) > - 1\) là
A. \(x = 0\).
B. \(x = 1\).
C. \(x = - 5\).
D. \(x = - 4\).
Giải mỗi bất phương trình sau:
a) \({\log _3}x < 2\)
b) \({\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge - 2\)
Cho hai ví dụ về bất phương trình logarit cơ bản.
Giải các bất phương trình lôgarit sau:
a) \({\rm{lo}}{{\rm{g}}_3}\left( {2x + 1} \right) \ge 2\);
b) \({\rm{lo}}{{\rm{g}}_2}\left( {3x - 1} \right) < {\rm{lo}}{{\rm{g}}_2}\left( {9 - 2x} \right)\);
c) \({\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left( {x + 1} \right) \le {\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left( {4\dot x - 5} \right)\);
d) \({\rm{lo}}{{\rm{g}}_2}\left( {2x - 1} \right) \le {\rm{lo}}{{\rm{g}}_4}{(x + 1)^2}\).
Nhắc lại rằng mức cường độ âm (đ̉o bằng \({\rm{dB}}\) ) được tính bởi công thức \({\rm{L}} = 10{\rm{log}}\frac{I}{{{I_0}}}\), trong đó \(I\)là cường độ âm tính theo \({\rm{W}}/{{\rm{m}}^2}\) và \({I_0} = {10^{ - 12}}{\rm{\;W}}/{{\rm{m}}^2}\).
a) Tính cường độ âm của âm thanh tàu điện ngầm có mức cường độ âm là 100 dB.
b) Âm thanh trên một tuyến đường giao thông có mức cường độ âm thay đồi từ \(70{\rm{\;dB}}\) đến \(85{\rm{\;dB}}\). Hỏi cường độ âm thay đổi trong đoạn nào?
Nhắc lại rằng độ pH của một dung dịch được tính bằng công thức \({\rm{pH}} = - {\rm{log}}\left[ {{{\rm{H}}^ + }} \right]\), ở đó \(\left[ {{{\rm{H}}^ + }} \right]\)là nồng độ ion hydrogen của dung dịch tính bằng mol/lít. Biết rằng máu của người bình thường có độ pH từ 7,30 đến 7,45. Hỏi nồng độ ion hydrogen trong máu người bình thường nhận giá trị trong đoạn nào?
Với giá trị nào của \(x\) thì đồ thị hàm số \(y = {\rm{lo}}{{\rm{g}}_{0,5}}x\) nằm phía trên trục hoành?
A. \(x > 0,5\).
B. \(x < 0,5\).
C. \(x > 1\).
D. \(0 < x < 1\).
Nghiệm của bất phượng trinh \({\rm{log}}2\left( {x + 1} \right) > 1\) là
A. \(x > 4\).
B. \( - 1 < x < 4\).
C. \(x > - \frac{1}{2}\).
D. \(x > \frac{e}{2} - 1\).
Tập nghiệm của bất phương trình \({\log _{0,2}}\left( {x + 1} \right) > - 3\) là:
A. \(\left( { - 1;124} \right).\)
B. \(\left( {124; + \infty } \right).\)
C. \(\left( { - 1; - \frac{{26}}{{27}}} \right).\)
D. \(\left( { - \infty ;124} \right).\)
Giải mỗi bất phương trình sau:
a) \({\log _{\frac{1}{2}}}\left( {2x - 6} \right) < - 3;\)
b) \({\log _3}\left( {{x^2} - 2x + 2} \right) > 0;\)
c) \({\log _4}\left( {2{x^2} + 3x} \right) \ge \frac{1}{2};\)
d) \({\log _{0,5}}\left( {x - 1} \right) \ge {\log _{0,5}}\left( {5 - 2x} \right);\)
e) \(\log \left( {{x^2} + 1} \right) \le \log \left( {x + 3} \right);\)
g)\({\log _{\frac{1}{5}}}\left( {{x^2} - 6x + 8} \right) + lo{g_5}\left( {x - 4} \right) > 0.\)
Mức cường độ âm L (dB) được tính bởi công thức \(L = 10{\rm{log}}\frac{I}{{{{10}^{ - 12}}}},\) trong đó\(I\left( {{\rm{W/}}{{\rm{m}}^{\rm{2}}}} \right)\)là cưởng độ âm. Để đảm bảo sức khoẻ cho công nhân, mức cường độ âm trong một nhà máy phải giữ sao cho không vượt quá 85 dB. Hỏi cường độ ẩm của nhà máy đó phải thoả mãn điều kiện nào để đảm bảo sức khoẻ cho công nhân?
Tập nghiệm của bất phương trình \({\log _2}\left( {3x - 1} \right) < 3\) là:
A. \(\left( { - \infty ;3} \right).\)
B. \(\left( {\frac{1}{3};3} \right).\)
C. \(\left( { - \infty ;\frac{{10}}{3}} \right).\)
D. \(\left( {\frac{1}{3};\frac{{10}}{3}} \right).\)
Giải các bất phương trình sau:
a) \({\log _3}\left( {x + 4} \right) < 2\);
b) \({\log _{\frac{1}{2}}}x \ge 4\);
c) \({\log _{0,25}}\left( {x - 1} \right) \le - 1\);
d) \({\log _5}\left( {{x^2} - 24x} \right) \ge 2\);
e) \(2{\log _{\frac{1}{4}}}\left( {x + 1} \right) \ge {\log _{\frac{1}{4}}}\left( {3x + 7} \right)\);
g) \(2{\log _3}\left( {x + 1} \right) \le 1 + {\log _3}\left( {x + 7} \right)\).
Tìm tất cả các số nguyên x thỏa mãn \({\log _3}\left( {x - 2} \right).{\log _3}\left( {x - 1} \right) < 0\).
Tìm tập xác định của hàm số:
a) \(y = f\left( x \right) = \sqrt {4 - {2^x}} + \frac{1}{{\sqrt {{{\log }_2}x} }}\);
b) \(y = f\left( x \right) = \sqrt {{{\log }_{\frac{1}{2}}}\left( {x - 2} \right)} \).
Gọi \(S\) là tập tất cả các giá trị nguyên của \(m\) sao cho bất phương trình có đúng 3 nghiệm nguyên. Số phần tử của \(S\) là:
Khi \(m = 2\), tập nghiệm của bất phương trình là:
Tập nghiệm của bất phương trình \({\log _2}\left( {x - 1} \right) < 3\) là:
Tập nghiệm của bất phương trình \(\log x \ge 1\) là
Tập nghiệm của bất phương trình \({\log _5}(x - 2) \le 1\) là
Số nghiệm nguyên của bất phương trình \({\log _3}(2 - x) \le 1\) là
Bất phương trình \({\log _{0,3}}(x - 1) \le {\log _{0,3}}(2x + 1)\) có tập xác định là












