Nội dung từ Loigiaihay.Com
Cho đường tròn (O;R) đường kính AB và điểm C thuộc đường tròn (O) (C khác A và B). Kẻ CH vuông góc với AB tại H.
a) Chứng minh \(\Delta ABC\) vuông tại C và \(C{H^2} = AC.BC.\sin A.\cos A\).
b) Tiếp tuyến tại A của đường tròn (O) cắt tia BC ở D. Gọi I là trung điểm của AD. Chứng minh đường thẳng IC là tiếp tuyến của đường tròn (O).
c) Tiếp tuyến tại B của đường tròn (O) cắt IC ở K. Xác định vị trí điểm C trên đường tròn (O) để diện tích tứ giác ABKI nhỏ nhất.
a) Chứng minh tam giác ACH và tam giác CHB vuông nên viết các hệ thức lượng liên quan đến cạnh CH.
Chứng minh \(\widehat {CAB} = \widehat {HCB}\) nên \(\cos \widehat {CAB} = \cos \widehat {HCB}\) suy ra điều phải chứng minh.
b) Chứng minh \(\Delta IAO = \Delta ICO\left( {c.c.c} \right)\) suy ra \(\widehat {IOA} = \widehat {ICO} = 90^\circ \) hay \(IC \bot OC\) tại C.
c) Chứng minh \(\Delta AIO = \Delta CIO\) và \(\Delta KCO = \Delta KBO\).
Biểu diễn \({S_{AIKB}}\) theo \({S_{\Delta IOK}}\).
Suy ra diện tích nhỏ nhất của \({S_{AIKB}}\) theo R.
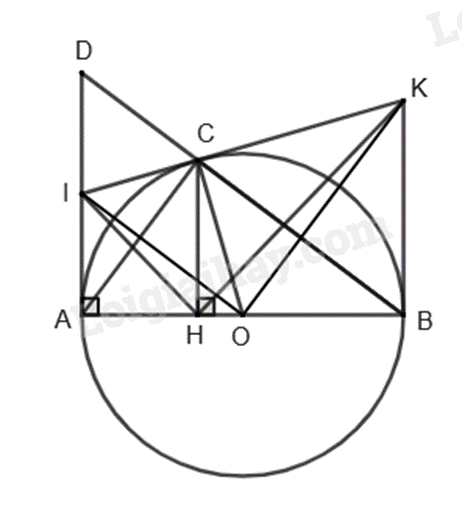
a) Vì AB là đường kính của (O) và \(C \in \left( O \right)\) suy ra \(\Delta ABC\) vuông tại C.
Vì CH vuông góc với AB tại H nên theo hệ thức lượng trong tam giác vuông, ta có:
\(CH = AC.\sin A\) (tam giác ACH vuông tại H)
và \(CH = BC.\cos \widehat {HCB}\) (tam giác CHB vuông tại H).
Mà \(\widehat {CAB} = \widehat {HCB}\) (cùng phụ với \(\widehat {ACH}\)) nên \(\cos \widehat {CAB} = \cos \widehat {HCB}\) hay \(\cos A = \cos \widehat {HCB}\). Do đó \(CH = BC.\cos A\).
Do đó \(C{H^2} = \left( {AC.\sin A} \right)\left( {BC.\cos A} \right) = AC.BC.\sin A.\cos A\).
b) Ta có \(CI = IA = ID\) (đường trung truyến trong tam giác vuông)
Xét tam giác IAO và tam giác ICO có:
AO = OC = R
IA = IC (cmt)
OI chung
Suy ra \(\Delta IAO = \Delta ICO\left( {c.c.c} \right)\), do đó \(\widehat {IOA} = \widehat {ICO} = 90^\circ \) hay \(IC \bot OC\) tại C.
Vậy IC là tiếp tuyến của (O) tại điểm C.
c) Theo ý b, ta có \(\Delta AIO = \Delta CIO\) (c.c.c).
Chứng minh tương tự, ta có \(\Delta KCO = \Delta KBO\) (c.c.c).
Mà \({S_{AIKB}} = {S_{\Delta AIO}} + {S_{\Delta CIO}} + {S_{\Delta COK}} + {S_{\Delta KOB}} = 2\left( {{S_{\Delta CIO}} + {S_{\Delta COK}}} \right)\)
Suy ra \({S_{AIKB}} = 2.{S_{\Delta IOK}} = OC.IK = R.IK \ge R.AB = R.2R = 2{R^2}\)
Dấu “=” xảy ra khi IK = AB. Khi đó C là điểm chính giữa $\overset\frown{AB}$.
Vậy \({S_{AIKB}}\) có giá trị lớn nhất là \(2{R^2}\) khi C là điểm chính giữa $\overset\frown{AB}$.

Các bài tập cùng chuyên đề
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD.
a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE.
b) Chứng minh rằng tứ giác ABCD là một hình thang cân.
c) Biết rằng \(AB = 12cm\) và \(\widehat {COD} = {100^o}\). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC.
d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
Cho tam giác vuông ABC (\(\widehat A = {90^o}\)) có \(\widehat C = {30^o}\) và AB=3cm. Đường phân giác của góc B cắt AC tại D.
a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC.
b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy.
c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB.
a) Xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (O’). Chứng minh ba điểm E, C, K thẳng hàng.
d) Chứng minh HK là tiếp tuyến của đường tròn (O’).
Cho đường tròn (O;R) , (O;R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.
a) Tứ giác BDCE là hình gì?
b) Gọi I là giao điểm của DA và đường tròn (O’). Chứng minh rằng ba điểm E, I, C thẳng hàng.
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O’).
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn, \(D \in \left( O \right)\) và \(E \in \left( {O'} \right)\). Gọi M là giao điểm của BD và CE.
a) Tính số đo của \(\widehat {DAE}\).
b) Tứ giác ADME là hình gì?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn.
Cho đường tròn \((O)\), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn \((O')\) có đường kính CB.
a) Kẻ dây DE của đường tròn \((O)\) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
b) Gọi K là giao điểm của DB và đường tròn \((O')\). Chứng minh rằng ba điểm E, C, K thẳng hàng;
c) Chứng minh HK là tiếp tuyến của đường tròn \((O')\).












