Nội dung từ Loigiaihay.Com
Mỗi buổi sáng, Nam thường đi xe đạp từ nhà đến trường với vận tốc 15 km/h và hết 20 phút. Hỏi quãng đường từ nhà Nam đến trường dài bao nhiêu ki lô mét?
Đổi thời gian phút ra giờ.
Quãng đường bằng vận tốc nhân thời gian.
20 phút = \(\dfrac{{20}}{{60}} giờ = \dfrac{1}{3}\) giờ.
Quãng đường từ nhà Nam đến trường là: \(15.\dfrac{1}{3} = \dfrac{{15}}{3} = 5km\)

Các bài tập cùng chuyên đề
Bài 1 :
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
-
A.
\(\dfrac{{ - 2}}{{27}}\)
-
B.
\(\dfrac{{ - 4}}{9}\)
-
C.
\(\dfrac{{ - 1}}{{18}}\)
-
D.
\(\dfrac{{ - 3}}{2}\)
Bài 2 :
Chọn câu sai.
-
A.
\(\dfrac{2}{7}.\dfrac{{14}}{6} = \dfrac{2}{3}\)
-
B.
\(25.\dfrac{{ - 4}}{{15}} = \dfrac{{ - 20}}{3}\)
-
C.
\({\left( {\dfrac{2}{{ - 3}}} \right)^2}.\dfrac{9}{4} = 1\)
-
D.
\(\dfrac{{ - 16}}{{25}}.\left( {\dfrac{{25}}{{ - 24}}} \right) = - \dfrac{2}{3}\)
Bài 3 :
Tìm số nguyên \(x\) biết \(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\)
-
A.
\(x \in \left\{ { - 3; - 2; - 1} \right\}\)
-
B.
\(x \in \left\{ { - 4; - 3; - 2; - 1} \right\}\)
-
C.
\(x \in \left\{ { - 3; - 2} \right\}\)
-
D.
\(x \in \left\{ { - 3; - 2; - 1;0} \right\}\)
Bài 4 :
Tính \(\dfrac{9}{{14}} \cdot \dfrac{{ - 5}}{8} \cdot \dfrac{{14}}{9}\)
-
A.
\(\dfrac{{ - 15}}{{28}}\)
-
B.
\(\dfrac{{ - 9}}{{28}}\)
-
C.
\(\dfrac{{ - 5}}{8}\)
-
D.
\(\dfrac{{ - 7}}{8}\)
Bài 5 :
Tính: \(\dfrac{6}{{25}}.\dfrac{{ - 15}}{4}\)
-
A.
\(\dfrac{{ 9}}{10}\)
-
B.
\(\dfrac{{ -10}}{{9}}\)
-
C.
\(\dfrac{{ - 9}}{{10}}\)
-
D.
\(\dfrac{{ 10}}{{9}}\)
Bài 6 :
Chọn câu sai.
-
A.
\(\dfrac{{ - 3}}{4}.\dfrac{{ - 4}}{5} = - \dfrac{3}{5}\)
-
B.
\(21.\dfrac{6}{7} = 18\)
-
C.
\({\left( {\dfrac{{ - 1}}{2}} \right)^2}.\dfrac{{16}}{5} = \dfrac{4}{5}\)
-
D.
\(\dfrac{{19}}{{28}}.\dfrac{{56}}{{57}} = \dfrac{2}{3}\)
Bài 7 :
Tìm số nguyên \(x\) biết \(\dfrac{{32}}{{15}}.\dfrac{{45}}{{16}} < x < \dfrac{{ - 8}}{3}.\dfrac{{ - 9}}{2}\)
-
A.
\(x \in \left\{ {7;8;9;10;11;12} \right\}\)
-
B.
\(x \in \left\{ {7;8;9;10;11} \right\}\)
-
C.
\(x \in \left\{ {6;12} \right\}\)
-
D.
\(x \in \left\{ {6;7;8;9} \right\}\)
Bài 8 :
Tính \(D = \dfrac{3}{7}.\dfrac{2}{5}.\dfrac{7}{3}.20.\dfrac{{19}}{{72}}\)
-
A.
\(\dfrac{{19}}{9}\)
-
B.
\(\dfrac{{ - 9}}{2}\)
-
C.
\(\dfrac{{ - 5}}{{18}}\)
-
D.
\(\dfrac{{ - 17}}{8}\)
Bài 9 :
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
-
A.
\(\dfrac{1}{{{2^{99}}}}\)
-
B.
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
-
C.
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
-
D.
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Bài 10 :
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\dfrac{5}{3}\)cm và \(\dfrac{7}{4}\)cm?
-
A.
\(\dfrac{{33}}{{24}}\,c{m^2}\)
-
B.
\(\dfrac{{35}}{{12}}c{m^2}\)
-
C.
\(\dfrac{{35}}{{24}}\,c{m^2}\)
-
D.
\(\dfrac{{33}}{{12}}\,c{m^2}\)
Bài 11 :
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\dfrac{2}{3}\)cm và \(\dfrac{15}{7}\)cm?
-
A.
\(\dfrac{{5}}{{7}}\,c{m^2}\)
-
B.
\(\dfrac{{5}}{{14}}c{m^2}\)
-
C.
\(\dfrac{{10}}{{7}}\,c{m^2}\)
-
D.
\(\dfrac{{118}}{{21}}\,c{m^2}\)
Bài 12 :

Điền số thích hợp vào ô trống
Bài 13 :
Tìm \(x\) biết:
\(x - \frac{1}{4} = \frac{7}{2}.\frac{{ - 3}}{5}\)
Bài 14 :
Em hãy nhớ lại quy tắc nhân hai phân số (có tử và mẫu đều dương), rồi tính \(\dfrac{8}{3}.\dfrac{3}{7}\) và \(\dfrac{4}{6}.\dfrac{5}{8}\).
Bài 15 :
Tính:
a) \(\dfrac{{ - 2}}{5}.\dfrac{5}{4}\)
b) \(\dfrac{{ - 7}}{{10}}.\dfrac{{ - 9}}{{11}}\)
Bài 16 :
Tính diện tích hình tam giác biết một cạnh dài \(\dfrac{9}{5}cm\) , chiều cao ứng với cạnh đó bằng \(\dfrac{7}{3}cm\).
Bài 17 :
Tính một cách hợp lí
B=\(\frac{5}{13}.\frac{8}{15} + \frac{5}{13}.\frac{26}{15} - \frac{5}{13}. \frac{8}{15}\)
Bài 18 :
Em hãy nhớ lại quy tắc nhân hai phân số (có tử và mẫu đều dương), rồi tính \(\dfrac{8}{3}.\dfrac{3}{7}\) và \(\dfrac{4}{6}.\dfrac{5}{8}\).
Bài 19 :
Tính:
a) \(\dfrac{{ - 2}}{5}.\dfrac{5}{4}\)
b) \(\dfrac{{ - 7}}{{10}}.\dfrac{{ - 9}}{{11}}\)
Bài 20 :
Tính diện tích hình tam giác biết một cạnh dài \(\dfrac{9}{5}cm\) , chiều cao ứng với cạnh đó bằng \(\dfrac{7}{3}cm\).
Bài 21 :
Tính:
a)\(\dfrac{6}{{13}}.\dfrac{8}{7}.\dfrac{{ - 26}}{3}.\dfrac{{ - 7}}{8}\)
b) \(\dfrac{6}{5}.\dfrac{3}{{13}} - \dfrac{6}{5}.\dfrac{{16}}{{13}}\)
Bài 22 :
Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\frac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Hỏi độ cao của đáy sông Sài Gòn là bao nhiêu mét?
Bài 23 :
Một mảnh vườn có diện tích 240 m, được trồng hai loại hoa là hoa cúc và hoa hồng. Phần diện tích trồng hoa cúc chiếm \(\frac{3}{4}\) diện tích cả vườn. Hỏi diện tích trồng hoa hồng là bao nhiêu mét vuông?
Bài 24 :
Tính tích và viết kết quả ở dạng phân số tối giản:
a) \(\frac{{ - 5}}{9}.\frac{{12}}{{35}}\);
b) \(\left( {\frac{{ - 5}}{8}} \right).\frac{{ - 6}}{{55}}\)
c) \(\left( { - 7} \right).\frac{2}{5}\);
d) \(\frac{{ - 3}}{8}.\left( { - 6} \right)\)
Bài 25 :
Tính tích và viết kết quả ở dạng phân số tối giản:
a) \(\frac{{ - 9}}{{10}}.\frac{{25}}{{12}};\)
b) \(\left( {\frac{{ - 3}}{8}} \right).\frac{{ - 12}}{5}.\)
Bài 26 :
Tính tích và viết kết quả ở dạng phân số tối giản:
a) \(8.\frac{{( - 5)}}{6};\)
b) \(\frac{5}{{21}}.( - 14).\)
Bài 27 :
Tính \(B = \frac{{{2^2}}}{3} \cdot \frac{{{3^2}}}{8} \cdot \frac{{{4^2}}}{{15}} \cdot \frac{{{5^2}}}{{24}} \cdot \frac{{{6^2}}}{{35}} \cdot \frac{{{7^2}}}{{48}} \cdot \frac{{{8^2}}}{{63}} \cdot \frac{{{9^2}}}{{80}}\) ta được
-
A.
\(\frac{9}{5}\)
-
B.
\(\frac{3}{5}\)
-
C.
\(3\)
-
D.
\(\frac{6}{5}\)
Bài 28 :
Tính giá trị biểu thức \(A = \left( {\frac{{11}}{4}.\frac{{ - 5}}{9} - \frac{4}{9}.\frac{{11}}{4}} \right).\frac{8}{{33}}\)
-
A.
\(A = - \frac{2}{3}\)
-
B.
\(A = \frac{2}{3}\)
-
C.
\(A = - \frac{3}{2}\)
-
D.
\(A = \frac{3}{2}\)
Bài 29 :
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\frac{5}{3}\, cm\) và \(\frac{7}{4}\, cm\)?
-
A.
\(\frac{{33}}{{24}}\,c{m^2}\)
-
B.
\(\frac{{35}}{{12}}c{m^2}\)
-
C.
\(\frac{{35}}{{24}}\,c{m^2}\)
-
D.
\(\frac{{33}}{{12}}\,c{m^2}\)
Bài 30 :
Tính diện tích hình chữ nhật \(ABCD\) ở hình sau:
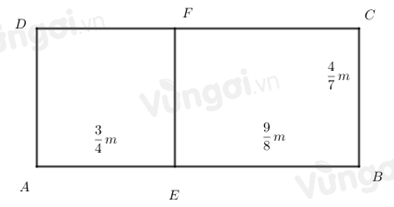
-
A.
\(\frac{{15}}{{14}}\,{m^2}\)
-
B.
\(\frac{{14}}{{15}}\,{m^2}\)
-
C.
\(\frac{{15}}{8}{m^2}\)
-
D.
\(\frac{4}{7}\,{m^2}\)












