Nội dung từ Loigiaihay.Com
Một người xách một xô nước đi trên đường, mỗi bước đi được 50 cm. Chu kì dao động riêng của nước trong xô là 1 s. Nước trong xô sóng sánh mạnh nhất khi người đó đi với tốc độ là bao nhiêu cm/s?
Vận dụng kiến thức về hiện tượng cộng hưởng
+ Chiều dài của mỗi bước chân: L=50cm
+ Tần số dao động riêng của nước trong xô: \({f_0} = \frac{1}{{{T_0}}} = 1Hz\)
+ Nước trong xô sóng sánh mạnh nhất khi nhịp bước của người có tần số trùng với tần số dao động riêng của nước trong xô. Vậy người đó bước đều với tần số: \(f = {f_0} = 1Hz \Rightarrow T = \frac{1}{f} = 1s\)
Nước trong xô sóng sánh mạnh nhất khi người đi với vận tốc: \({\rm{\;}}v = \frac{s}{t} = \frac{L}{T} = \frac{{50}}{1} = 50\left( {cm/s} \right)\)
Đáp án: 50

Các bài tập cùng chuyên đề
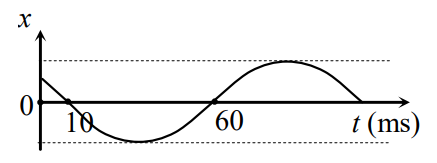
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
Đồ thị li độ - thời gian của một con lắc đơn dao động điều hoà được mô tả trên Hình 1.3.
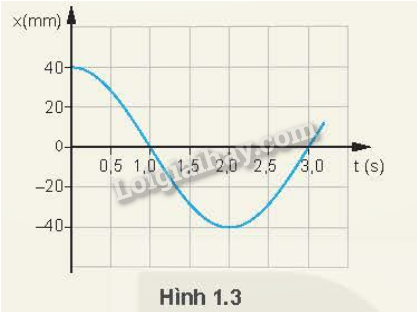
1. Hãy mô tả dao động điều hoà của con lắc đơn.
2. Xác định biên độ và li độ của con lắc ở các thời điểm \(t = 0,{\rm{ }}t = 0,5\;s,{\rm{ }}t = 2,0\;s\).
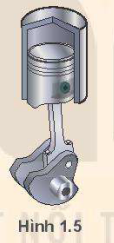
Pít-tông của một động cơ đốt trong dao động trên một đoạn thẳng dài \(16\;cm\) và làm cho trục khuỷu của động cơ quay đều (Hình 1.5). Xác định biên độ dao động của một điểm trên mặt pít-tông.
Để vẽ đồ thị hoặc viết phương trình của một dao động điều hòa cần biết những đại lượng vật lí nào?
Hình 2.1 là đồ thị dao động điều hoà của một vật.
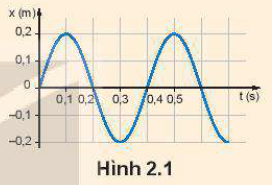
Hãy xác định:
- Biên độ, chu kì, tần số của dao động.
- Nêu thời điểm mà vật có li độ \(x = 0;x = 0,1\;m\).
Từ hình 2.1 hãy xác định tần số góc của dao động của vật.
Hình 2.3 là đồ thị dao động điều hoà của một con lắc.
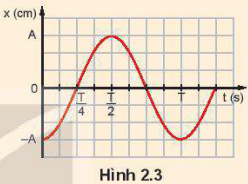
Hãy cho biết:
- Vị trí và hướng dịch chuyển của con lắc tại thời điểm ban đầu.
- Pha ban đầu của dao động.
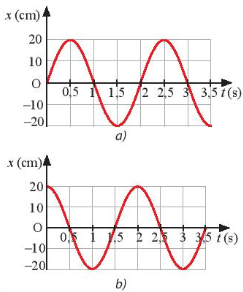
Hai con lắc 1 và 2 dao động điều hoà tại cùng thời điểm quan sát vị trí của chúng được biểu diễn trên Hình 2.5a, b. Hỏi dao động của con lắc nào sớm pha hơn và sớm hơn bao nhiêu?

1. Một vật dao động điều hoà có biên độ 10cm, tần số 5Hz. Tại thời điểm ban đầu \(\left( {t = 0} \right)\) vật ở vị trí biên.
- Xác định chu kì, tần số góc, pha ban đầu của dao động.
- Viết phương trình và vẽ đồ thị \(\left( {x - t} \right)\) của dao động.
2. Cho hai con lắc đơn dao động điều hoà. Biết phương trình dao động của con lắc thứ nhất là \(x = 20\cos \left( {20\pi t + \frac{\pi }{2}} \right)(cm)\). Con lắc thứ hai có cùng biên độ và tần số nhưng lệch về thời gian so với con lắc thứ nhất một phần tư chu kì. Viết phương trình dao động của con lắc thứ hai.
1. Đại lượng nào dưới đây đặc trưng cho độ lệch về thời gian giữa hai dao động điều hoà cùng chu kì?
A. Li độ. B. Pha. C. Pha ban đầu. D. Độ lệch pha.
2. Hãy chứng minh rằng độ lệch pha giữa hai dao động điều hoà cùng tần số là đại lượng không đổi và bằng độ lệch pha ban đầu.
Trong bài học trước, chúng ta đã tìm hiểu dao động điều hòa và định nghĩa các đại lượng mô tả dao động điều hòa. Trong bài học này, chúng ta sẽ sử dụng các đại lượng đó để mô tả một số dao động điều hòa thường gặp trong cuộc sống.
Ở Hình 2.1 trong điều kiện không có lực cản, dao động của quả cầu với biên độ nhỏ là một ví dụ về dao động điều hòa. Mô tả dao động điều hòa này như thế nào?
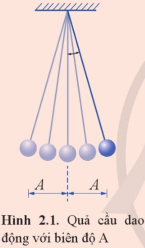
Con lắc đơn trong đồng hồ quả lắc Hình 2.2 gồm một thanh nhẹ có chiều dài 0,994 m. Tính chu kì dao động của con lắc nếu đồng hồ được đặt ở nơi có gia tốc rơi tự do g =9,8 m/s2.

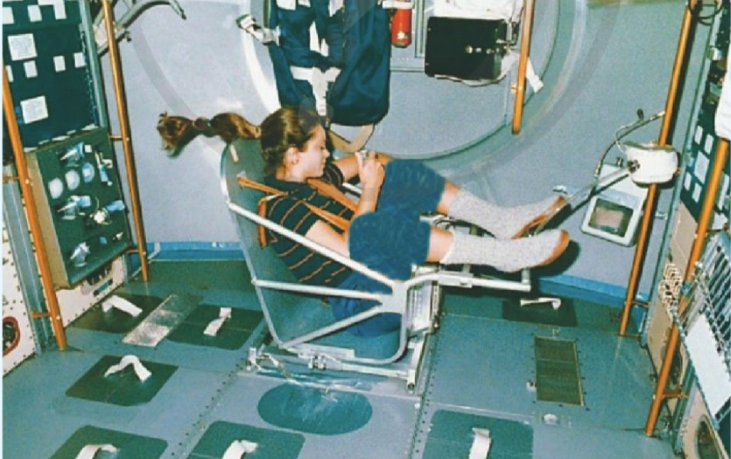
Khi làm việc dài ngày trên các trạm không gian vũ trụ, việc theo dõi các chỉ số sức khỏe như chiều cao, khối lượng cơ thể của các nhà du hành vũ trụ là rất quan trọng. Hình 2.7 chụp cảnh một nhà du hành vũ trụ đang ngồi trên dụng cụ đo khối lượng được lắp đặt tại trạm vũ trụ Skylab 2.
Dụng cụ này được thiết kế để cho phép các nhà du hành xác định khối lượng của họ ở điều kiện không trọng lượng. Nó là một cái ghế có khối lượng 12,47 kg gắn ở đầu một lò xo có độ cứng k = 605,6 N/m. Đầu kia của lò xo được gắn vào một điểm cố định của trạm.
Một máy đếm điện tử được kết nối với chiếc ghế có thể đo được chu kì dao động của ghế. Một nhà du hành ngồi trên ghế và đo được chu kì dao động là 2,08832 s. xác định khối lượng của người đó.
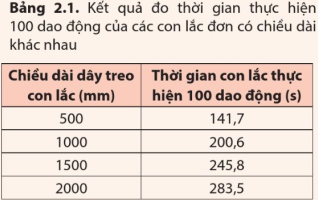
Một ứng dụng quan trọng của con lắc đơn là trong lĩnh vực địa chất. Các nhà địa chất quan tâm đến những tính chất đặc biệt của lớp bề mặt Trái Đất và thường xuyên phải đo gia tốc rơi tự do ở một nơi nào đó. Ví dụ như trầm tích khoáng sản hay các mỏ quặng có thể làm thay đổi giá trị gia tốc rơi tự do tại nơi đó. Nhờ vậy, các nhà địa chất đo gia tốc rơi tự do để phát hiện các vị trí có mở quặng. Một máy đo gia tốc rơi tự do đơn giản nhất chính là một con lắc đơn. Đo thời gian con lắc đơn có chiều dài l thực hiện một số dao động, từ đó suy ra chu kì T. Sau đó tính g dựa vào cộng thức (2.1). Lặp lại thí nghiệm nhiều lần với các con lắc cí chiều dài dây treo khác nhau. Lấy giá trị trung bình g ở các lần đo, ta được gia tốc rơi tự do tại đó.
Trong thí nghiệm đo gia tốc rơi tự do tại một địa phương, các nhà địa chất sử dụng đồng hồ để đo thời gian các con lắc đơn có chiều dài khác nhau thực hiện 100 chu kì dao động. Kết quả đo được cho trong Bảng 2.1. Xác định gia tốc rơi tự do tại địa phương đó.
1. Từ một số dụng cụ đơn giản như: lò xo nhẹ, dây nhẹ không dãn, vật nặng và giá đỡ.
a) Em hãy thực hiện hai thí nghiệm sau:
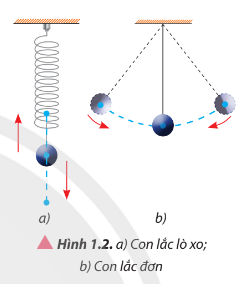
– Cố định một đầu của lò xo, gần vật nặng vào đầu còn lại của lò xo như Hình 1.2a. Kéo vật nặng xuống một đoạn theo phương thẳng đứng và buông nhẹ.
– Cố định một đầu của dây nhẹ không dãn, gắn vật nặng vào đầu còn lại của dây. Kéo vật nặng để dây treo lệch một góc xác định và buông nhẹ.
b) Quan sát và mô tả chuyển động của các vật, nêu điểm giống nhau về chuyển động của chúng.
2. Nêu một số ví dụ về dao động tuần hoàn.
3. Hãy nêu một ứng dụng của dao động tuần hoàn trong cuộc sống.
Nêu một số ví dụ về các vật dao động tự do trong thực tế.
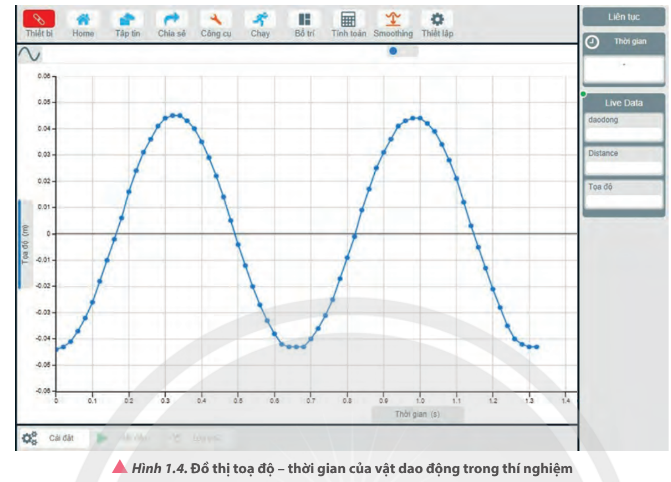
Nhận xét về hình dạng đồ thị tọa độ - thời gian của vật dao động trong Hình 1.4.
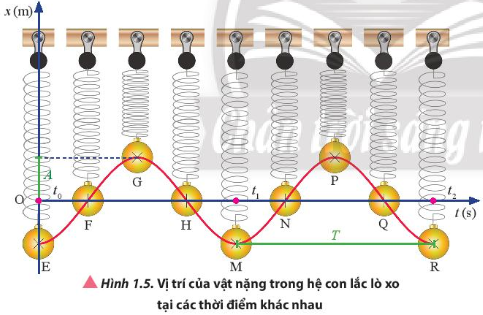
Quan sát Hình 1.5 và chỉ ra những điểm:
a) Có tọa độ dương, âm hoặc bằng 0.
b) Có khoảng cách đến vị trí cân bằng cực đại.
c) Gần nhau nhất có cùng trạng thái chuyển động.
Một con ong mật đang bay tại chỗ trong không trung (Hình 1.6), đập cánh với tần số khoảng 300 Hz. Xác định số dao động mà cánh ong mật thực hiện trong 1s và chu kì dao động của cánh ong.
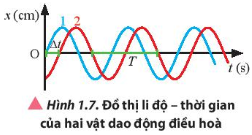
Quan sát Hình 1.7, so sánh biên độ và li độ của hai dao động 1 và 2 tại mỗi thời điểm.
Dựa vào dữ kiện trong câu Thảo luận 6, xác định tần số góc khi ong đập cánh. Xem biên độ dao động của cánh ong là không đổi.
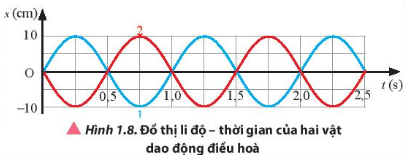
Quan sát đồ thị li độ - thời gian của hai dao động điều hòa được thể hiện trong Hình 1.8. Hãy xác định biên độ, chu kì, tần số, tần số góc của mỗi vật dao động và độ lệch pha giữa hai dao động.
Xác định độ lệch pha dao động trong Hình 1.9.
Xét vật thứ nhất bắt đầu dao động điều hòa từ vị trí cân bằng, vị trí thứ hai dao động điều hòa với biên độ lớn gấp hai lần, cùng chu kì và lệch pha Δφ=\(\frac{\pi }{4}\)rad so với vật thứ nhất. Vẽ phác đồ thị li độ - thời gian của hai vật trong hai chu kì dao động đầu tiên.
Tìm hiểu và trình bày một số ứng dụng thực tiễn của hiện tượng dao động.
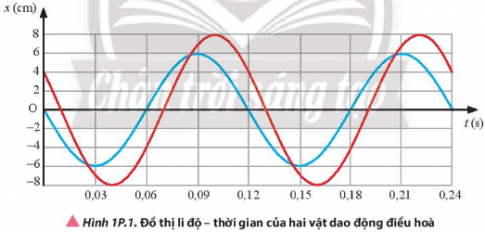
Xác định biên độ, chu kì, tần số, tần số góc của mỗi dao động và độ lệch pha giữa hai dao động có đồ thị li độ - thời gian như trong Hình 1P.1.
Vẽ phác đồ thị li độ – thời gian của hai dao động điều hoà trong các trường hợp:
a) Cùng biên độ, chu kì của dao động thứ nhất bằng ba lần chu kì của dao động thứ hai.
b) Biên độ của dao động thứ nhất bằng hai lần biên độ của dao động thứ hai, cùng chu kì, cùng pha.
c) Cùng biên độ, cùng chu kì và có độ lệch pha là π rad.
Chu kì dao động là:
A. Thời gian chuyển động của vật
B. Thời gian vật thực hiện được một dao động toàn phần
C. Số dao động toàn phần mà vật thực hiện được
D. Số dao động toàn phần mà vật thực hiện được trong một giây
Khi vật thực hiện được một dao động tương ứng với pha dao động sẽ thay đổi một lượng:
A. \(0rad\)
B. \(\frac{\pi }{2}rad\)
C. \(\pi rad\)
D. \(2\pi rad\)












