Nội dung từ Loigiaihay.Com
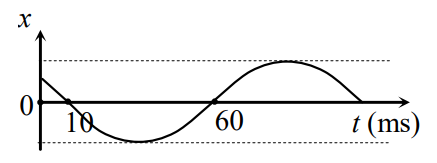
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
-
A.
0,06 s.
-
B.
0,12 s.
-
C.
0,1 s.
-
D.
0,05 s.
Sử dụng kĩ năng đọc đồ thị
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được \(\frac{1}{2}\) chu kì:
\(\frac{T}{2} = 60 - 10 \Rightarrow T = 100\,\,\left( {ms} \right) = 0,1\,\,\left( s \right)\)
Đáp án : C

Các bài tập cùng chuyên đề
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. $A$ được gọi là:
Một vật dao động điều hoà theo phương trình \(x = 2cos\left( {5\pi t + \frac{{7\pi }}{3}} \right)cm\). Biên độ dao động của vật là:
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
Một chất điểm dao động điều hoà trên quỹ đạo $MN = 30 cm$, biên độ dao động của vật là:
Một vật dao động điều hòa với phương trình $x=Acos(ωt+φ)$. Pha dao động tại thời điểm $t$ là:
Một vật dao động điều hòa theo phương trình x = 3cos(7πt + π) cm, pha dao động tại thời điểm t = 1 (s) là:
Một vật dao động điều hoà theo phương trình \(x = {\rm{ }}-5cos(5\pi t{\rm{ }} - 7\pi /6)cm\). Biên độ dao động và pha ban đầu của vật là:
Một vật dao động điều hòa thực hiện được N dao động trong thời gian ∆t giây. Chu kỳ dao động của vật là:
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\), chu kỳ dao động của chất điểm được xác định bởi:
Một vật dao động điều hòa trong thời gian $20$ giây vật thực hiện được $80$ dao động toàn phần. Chu kỳ dao động của vật là:
Một con lắc lò xo dao động với phương trình $x = 6c{\text{os}}\left( {20\pi t } \right)cm$. Xác định chu kỳ, tần số dao động của chất điểm.
Chất điểm dao động điều hòa với phương trình \(x = 6cos\left( {10t - \dfrac{{3\pi }}{2}} \right)cm\). Li độ của chất điểm khi pha dao động bằng \(\dfrac{{2\pi }}{3}\) là:
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức vận tốc tức thời của chất điểm là:
Một vật dao động điều hòa có phương trình \(x = 2cos\left( {2\pi t - \frac{{7\pi }}{6}} \right){\rm{ }}cm\). Li độ của vật tại thời điểm $t = 0,25 (s)$ là:
Một chất điểm dao động điều hòa với phương trình $x = Ac{\text{os}}\left( {\omega t + \varphi } \right)$. Tốc độ cực đại vật đạt được trong quá trình dao động là:
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5cos(7\pi t{\rm{ }} + \dfrac{{7\pi }}{6})cm\). Biểu thức vận tốc tức thời của chất điểm là:
Một chất điểm dao động điều hòa với phương trình \(x = Acos(\omega t + \varphi )\). Biểu thức gia tốc tức thời của chất điểm là:
Biểu thức nào sau đây là biểu thức tính gia tốc của một vật dao động điều hòa?
Một vật dao động điều hoà chu kỳ T. Gọi \({v_{max}}\) và \({a_{max}}\) tuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa \({v_{max}}\) và \({a_{max}}\) là:
Một chất điểm dao động điều hòa có tần số góc \(\omega \), tại thời điểm t chất điểm có li độ \(x{\rm{ }}\left( {cm} \right)\) và vận tốc \(v{\rm{ }}\left( {cm/s} \right)\). Biên độ dao động điều hòa của chất điểm là:












