Nội dung từ Loigiaihay.Com
Cho khối lăng trụ tam giác \(ABC.A'B'C'\) (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.
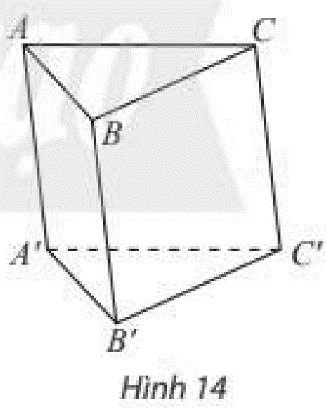
Chia khối lăng trụ thành ba khối chóp có đáy là một trong hai đáy của lăng trụ, đỉnh nằm trên đáy còn lại.
Chia khối lăng trụ tam giác \(ABC.A'B'C'\) thành ba khối chóp: \(A.A'B'C',B'.ABC\) và \(C.A'B'C'\).

Các bài tập cùng chuyên đề
Cho khối lăng trụ đứng ABC.A'B'C' có AA' = 5 cm, AB = 6 cm, BC = 2 cm, \(\widehat {ABC} = {150^0}.\) Tính thể tích của khối lăng trụ.
Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.

Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tinh thể tích của khối lăng trụ.
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng \(a\) là
A. \(\frac{{{a^3}\sqrt 3 }}{4}\).
B. \(\frac{{{a^3}\sqrt 3 }}{3}\).
C. \(\frac{{{a^3}\sqrt 2 }}{3}\).
D. \(\frac{{{a^3}\sqrt 2 }}{2}\).
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy ABCD là hình chữ nhật. Biết \(AC = AA' = 2a\). Giá trị lớn nhất của thể tích hình hộp \(ABCD.A'B'C'D'\) bằng
A. \(8{a^3}\).
B. \(6{a^3}\).
C. \(4{a^3}\).
D. \({a^3}\).
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = 1,AA' = 2\). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
A. \(\frac{{\sqrt 3 }}{2}\).
B. \(\frac{{\sqrt 3 }}{6}\).
C. \(\frac{{\sqrt 3 }}{4}\).
D. \(\frac{{\sqrt 3 }}{8}\).
Tính thể tích của khối lăng trụ \(ABC.A'B'C'\)' biết tất cả các cạnh bằng \(a\) và hình chiếu của \(A'\) trên mặt phẳng \(\left( {ABC} \right)\) là trung điểm của \(AB\).
Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.
Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3 g/cm.
Cho khối lăng trụ có diện tích đáy bằng \({a^2}\) và chiều cao bằng \(3a\). Thể tích của khối lăng trụ đó bằng:
A. \({a^3}\).
B. \(3{a^3}\).
C. \(\frac{{{a^3}}}{3}\).
D. \(9{a^3}\).
Cho hình lăng trụ \ABC.A'B'C' có A'B'C' và AA'C' là hai tam giác đều cạnh a. Biết \(\left( {ACC'A'} \right) \bot \left( {A'B'C'} \right)\). Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
Cho hình lăng trụ đều ABC. A’B’C’ có cạnh đáy bằng a. Biết \(d\left( {A,\left( {A'BC} \right)} \right) = \frac{{a\sqrt {57} }}{{12}}\). Tính \({V_{ABC.A'B'C'}}\).
Cho lăng trụ đứng ABC.A’B’C’ có đáy tam giác ABC vuông tại B, \(AB = 2a,BC = a,AA' = 2a\sqrt 3 \). Thể tích khối lăng trụ ABC.A’B’C’ là
A. \(4{a^3}\sqrt 3 \)
B. \(2{a^3}\sqrt 3 \)
C. \(\frac{{2{a^3}\sqrt 3 }}{3}\)
D. \(\frac{{4{a^3}\sqrt 3 }}{3}\)
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B. Biết \(AB = a,BC = a\sqrt 3 \), góc giữa hai mặt phẳng (C’AB) và (ABC) bằng \({60^0}\). Tính \({V_{ABC.A'B'C'}}\)
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với \(AB = AC = a,\widehat {BAC} = {120^0}\), mặt phẳng (AB’C’) tạo với đáy một góc \({60^0}\). Tính thể tích V của khối lăng trụ đã cho.
Cho hình lăng trụ \(ABC \cdot A'B'C'\) có \(AA'B'C'\) là hình tứ diền đều cạnh bằng \(a\). Thể tích khối lăng trụ \(ABC \cdot A'B'C'\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\).
B. \(\frac{{{a^3}\sqrt 2 }}{4}\).
C. \(\frac{{{a^3}\sqrt 6 }}{3}\).
D. \(\frac{{{a^3}\sqrt 6 }}{{12}}\).
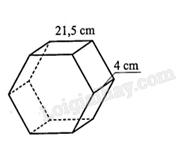
Người ta cần đổ bê tông để làm những viên gạch có dạng khối lăng trụ lục giác đều như hình bên với chiều cao là 4 cm và cạnh lục giác dài 21,5 cm. Tính thể tích bê tông theo đơn vị centimét khối để làm một viên gạch như thế (làm tròn kết quả đến hàng phần mười).
Cho khối lăng trụ có diện tích đáy \(S = 10\) \(c{m^2}\), cạnh bên có độ dài bằng 10 cm và tạo với mặt đáy một góc bằng \({60^o}\). Thể tích khối lăng trụ đã cho là
Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 .\) Tính thể tích V của khối lăng trụ.
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, AB = AC = 1, AA' = 2. Thể tích khối lăng trụ đã cho bằng
Khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \) và chiều cao bằng \(2a\sqrt 3 \). Thể tích khối lăng trụ đã cho bằng












