Nội dung từ Loigiaihay.Com
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
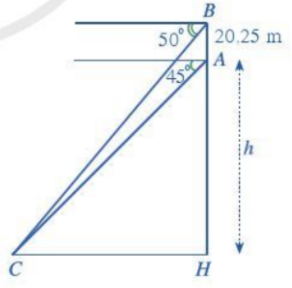
Bước 1: Tính \(\widehat {ACH},\widehat {BCH}\)
Bước 2: Tính \(\tan \widehat {ACH},\tan \widehat {BCH}\) theo h.
Bước 3: Giải phương trình ẩn h và kết luận.
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

Các bài tập cùng chuyên đề
Trong các khẳng định sau, khẳng định nào đúng?
Giá trị của biểu thức $S = 3 - {\rm{si}}{{\rm{n}}^2}{\rm{9}}{0^0} + {\rm{ 2co}}{{\rm{s}}^2}{\rm{6}}{{\rm{0}}^0}{\rm{ - 3ta}}{{\rm{n}}^2}{45^0}$ bằng:
Giá trị $\cot \dfrac{{89\pi }}{6}$ là
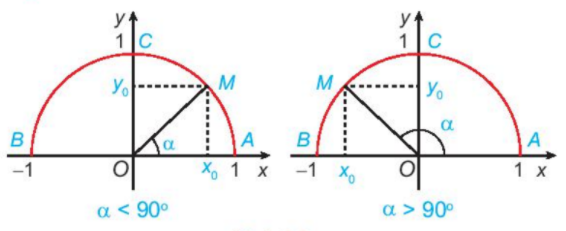
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Cho góc \(\alpha \;\;({0^o} < \alpha < {180^o})\) thỏa mãn \(\tan \alpha = 3\)
Tính giá trị biểu thức: \(P = \frac{{2\sin \alpha - 3\cos \alpha }}{{3\sin \alpha + 2\cos \alpha }}\)
Tìm các giá trị lượng giác của góc \({135^o}\)
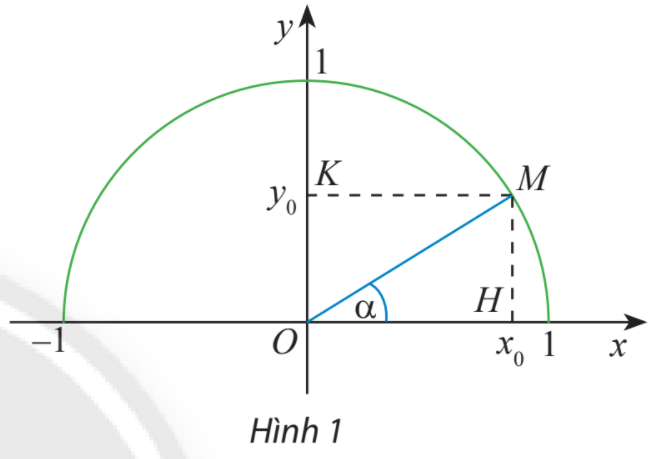
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
Cho góc \(\alpha \) tù. Khẳng định nào sau đây đúng?
Cho góc \(\alpha \) nhọn. Khẳng định nào sau đây đúng?
Tam giác \(ABC\) có \(\widehat A = {15^ \circ },\,\,\widehat B = {45^ \circ }.\) Giá trị của \(\tan C\) bằng:
A. \( - \sqrt 3 .\)
B. \(\sqrt 3 .\)
C. \(\frac{1}{{\sqrt 3 }}.\)
D. \( - \frac{1}{{\sqrt 3 }}.\)
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^ \circ }.\) Tích hoành độ và tung độ của điểm \(M\) bằng
A. \(\frac{1}{{2\sqrt 2 }}.\)
B. \(\frac{1}{2}\)
C. \( - \frac{1}{2}\)
D. \( - \frac{1}{{2\sqrt 2 }}.\)
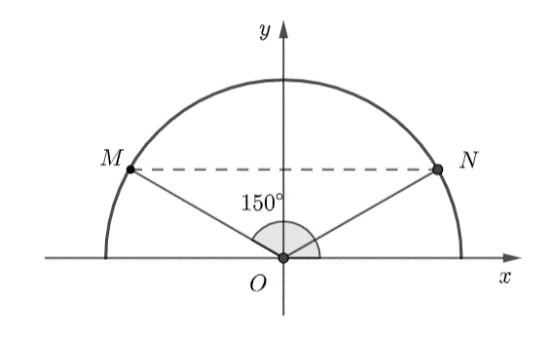
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }.\) \(N\) là điểm đối xứng với \(M\) qua trục tung. Giá trị của \(\tan \widehat {xON}\) bằng:
A. \(\frac{1}{{\sqrt 3 }}.\)
B. \( - \frac{1}{{\sqrt 3 }}.\)
C. \(\sqrt 3 .\)
D. \( - \sqrt 3 .\)
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diện tích của tam giác \(AOM\) bằng:
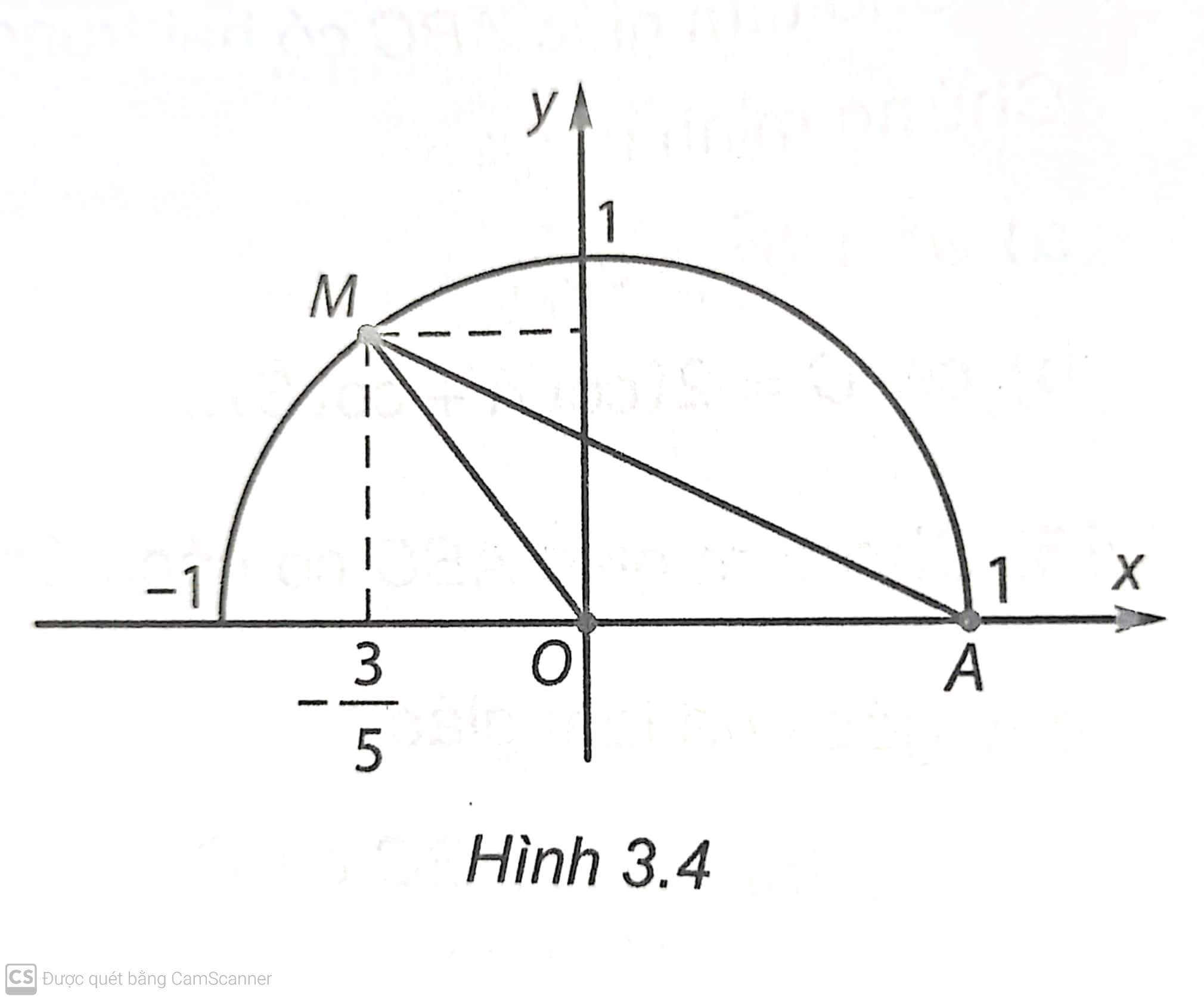
A. \(\frac{4}{5}.\)
B. \(\frac{2}{5}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{3}{{10}}.\)
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }\)(H.3.5). \(N\) là điểm đối xứng với \(M\) qua trục tung. Diện tích của tam giác \(MAN\) bằng:
A. \(\frac{{\sqrt 3 }}{4}.\)
B. \(\frac{{\sqrt 3 }}{2}.\)
C. \(\sqrt 3 .\)
D. \(2\sqrt 3 .\)
Tính giá trị của \(T = 4\cos 60^\circ + 2\sin 135^\circ + 3\cot 120^\circ \).
Cho 00 < \(\alpha \) < 1800. Chọn câu trả lời đúng
A. cos\(\alpha \) < 0
B. sin\(\alpha \) > 0
C. tan\(\alpha \) < 0
D. cot\(\alpha \) > 0
Cho tam giác ABC cân tại A có \(\widehat A = 120^\circ \). Khi đó sin B bằng
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \) .












