Nội dung từ Loigiaihay.Com
Tìm
a) \(\int {{3^x}dx} \)
b) \(\int {{e^{2x}}dx} \)
Sử dụng các công thức \(\int {{e^x}dx} = {e^x} + C\) và \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\)
a) \(\int {{3^x}dx} = \frac{{{3^x}}}{{\ln 3}} + C\)
b) \(\int {{e^{2x}}dx} = \int {{{\left( {{e^2}} \right)}^x}dx} = \frac{{{{\left( {{e^2}} \right)}^x}}}{{\ln \left( {{e^2}} \right)}} + C = \frac{{{e^{2x}}}}{2} + C\).

Các bài tập cùng chuyên đề
Tìm:
a) \(\int {{4^x}dx} \);
b) \(\int {\frac{1}{{{e^x}}}dx} \);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \).
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
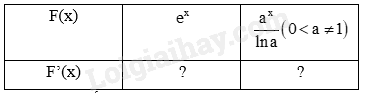
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Họ tất cả các nguyên hàm của hàm số \(2{e^x}\) là
A. \(2x{e^x} + C\).
B. \( - 2{e^x} + C\).
C. \(2{e^x}\).
D. \(2{e^x} + C\).
Nguyên hàm F(x) của hàm số \(f\left( x \right) = {e^x} - 3{e^{ - x}}\) thỏa mãn \(F\left( 0 \right) = 4\) là
A. \(F\left( x \right) = {e^x} - 3{e^{ - x}}\).
B. \(F\left( x \right) = {e^x} + 3{e^{ - 2x}}\).
C. \(F\left( x \right) = {e^x} + 3{e^{ - x}}\).
D. \(F\left( x \right) = {e^x} + 3{e^{ - x}} + 4\).
Tính đạo hàm của hàm số \(F(x) = \frac{{{a^x}}}{{\ln a}}(a > 0,a \ne 1)\). Từ đó, nêu một nguyên hàm của hàm số \(f(x) = {a^x}\)
\(\int {{7^x}dx} \) bằng:
A. \({7^x}.\ln 7 + C\)
B. \(\frac{{{7^{x + 1}}}}{{x + 1}} + C\)
C. \(\frac{{{7^x}}}{{\ln 7}} + C\)
D. \({7^x} + C\)
a) Tìm đạo hàm của các hàm số \(y = {e^x}\), \(y = \frac{{{a^x}}}{{\ln a}}\) với \(a > 0\), \(a \ne 1\).
b) Từ đó, tìm \(\int {{e^x}dx} \) và \(\int {{a^x}dx} \) (\(a > 0\), \(a \ne 1\)).
Khẳng định nào sau đây đúng?
A. \(\int {{3^{2x}}dx} = \frac{{{9^x}}}{{\ln 9}} + C\)
B. \(\int {{3^{2x}}dx} = {9^x}.\ln 9 + C\)
C. \(\int {{3^{2x}}dx} = {\left( {\frac{{{3^x}}}{{\ln 3}}} \right)^2} + C\)
D. \(\int {{3^{2x}}dx} = {3^x}.\ln 3 + C\)
Tìm:
a) \(\int {{{\left( {{2^x} + {3^x}} \right)}^2}{\rm{ }}} dx\);
b) \(\int {{{\left( {{e^x} - {e^{ - x}}} \right)}^2}} {\rm{ }}dx\).
\(\int {{{17}^x}dx} \) bằng:
A. \({17^x}\ln 17\).
B. \(\frac{{{{17}^x}}}{{\ln 17}}\).
C. \({17^x}\ln 17 + C\).
D. \(\frac{{{{17}^x}}}{{\ln 17}} + C\).
Chọn đáp án đúng.
Phát biểu nào sau đây đúng?
A. \(\int {{3^{2{\rm{x}}}}dx} = {9^x}.\ln 9 + C\).
B. \(\int {{3^{2{\rm{x}}}}dx} = \frac{{{9^x}}}{{2\ln 3}} + C\).
C. \(\int {{3^{2{\rm{x}}}}dx} = {\left( {\frac{{{3^x}}}{{\ln 3}}} \right)^2} + C\).
D. \(\int {{3^{2{\rm{x}}}}dx} = \frac{{{3^{2x}}}}{{\ln 3}} + C\).
Họ các nguyên hàm của hàm số \(f(x) = {e^x} + x\) là
Họ các nguyên hàm của hàm số \(f(x) = {10^x}\) là
Nguyên hàm của hàm số \(f\left( x \right) = {e^x}\) là
Nguyên hàm của hàm số \(y = {2^x}\) là
Nguyên hàm của hàm số \(f(x) = {3^x}\) là
Nguyên hàm của hàm số f(x) = \({e^x}\) là
Nguyên hàm của hàm số \(f\left( x \right) = {3^x}\) là
Họ tất cả các nguyên hàm của hàm số \(y = {3^{2x + 1}}\) là












