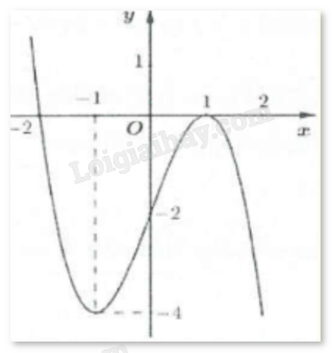
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng

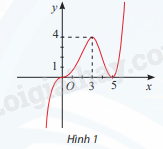
A. (5; $+ \infty$).         B. (3; 5).      C. (0; 5).      D. (3; $+ \infty$).

 

Bất phương trình $\sqrt {2{x^3} + 3{x^2} + 6x + 16}  - \sqrt {4 - x}  \geqslant 2\sqrt 3$ có tập nghiệm là $\left[ {a;b} \right].$ Hỏi tổng $a + b$ có giá trị là bao nhiêu?

Cho phương trình ${x^3} + \left( {m - 12} \right)\sqrt {4x - m}  = 4x\left( {\sqrt {4x - m}  - 3} \right)$, với $m$ là tham số. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt?

Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và đồ thị hàm số $y = f\left( x \right)$ như hình vẽ bên. Tìm số điểm cực trị của hàm số $y = {2019^{f\left( {f\left( x \right) - 1} \right)}}$.

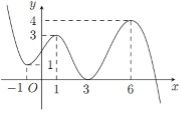
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)$ với mọi $x \in \mathbb{R}$. Có bao nhiêu số nguyên $m$ thuộc đoạn $\left[ { - 2019;\,2019} \right]$ để hàm số $g\left( x \right) = f\left( {1 - x} \right)$ nghịch biến trên khoảng $\left( { - \infty ;\, - 1} \right)$?

Cho bất phương trình $\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m$. Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình nghiệm đúng với mọi $x > 1.$

Cho hàm số đa thức $f(x)$ có đạo hàm tràm trên $R$. Biết $f(0) = 0$ và đồ thị hàm số $y = f'\left( x \right)$ như hình sau.

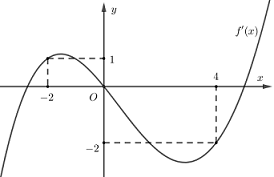
Hàm số $g(x) = \left| {4f(x) + {x^2}} \right|$ đồng biến trên khoảng nào dưới đây?

Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}$, có đồ thị $f\left( x \right)$ như hình vẽ. Hàm số $g\left( x \right) = f\left( {{x^3} + x} \right)$ đạt cực tiểu tại điểm ${x_0}$. Giá trị  ${x_0}$ thuộc khoảng nào sau đây?

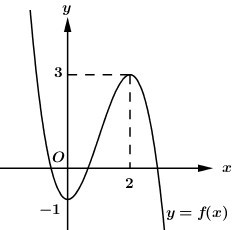
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị $f'\left( x \right)$ như hình vẽ bên. Số điểm cực đại của hàm số $g\left( x \right) = f\left( { - {x^2} + x} \right)$ là:

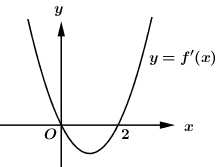
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và $f\left( 1 \right) = 1$. Đồ thị hàm số $y = f'\left( x \right)$ như hình bên. Có bao nhiêu số nguyên dương a để hàm số $y = \left| {4f\left( {\sin x} \right) + \cos 2x - a} \right|$ nghịch biến trên $\left( {0;\dfrac{\pi }{2}} \right)$?

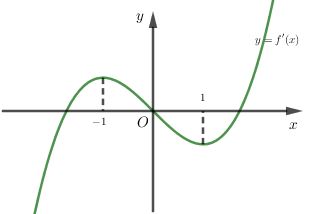
Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$. Đồ thị hàm số $y = f'\left( x \right)$ như hình bên. Hàm số $y = f\left( {{x^2} + 4x} \right) - {x^2} - 4x$ có bao nhiêu điểm cực trị thuộc khoảng $\left( { - 5;1} \right)$?

Số điểm cực trị của hàm số $y = \left| {{x^2} - 3x + 2} \right|$ là:

Số điểm cực trị của hàm số $y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|$ là:

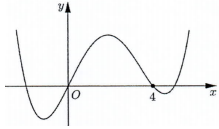
Cho hàm số bậc bốn $y = f\left( x \right)$ có đồ thị như hình bên. Số điểm cực trị của hàm số $g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)$ là:

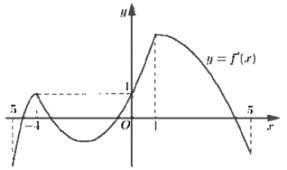
Cho hàm số $y = f\left( x \right)$. Hàm số $y = f'\left( x \right)$ có đồ thị như hình vẽ bên.

Hàm số $y = f\left( {{x^2} - 1} \right)$ có bao nhiêu điểm cực trị?

Cho hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {x - 3} \right)$. Điểm cực đại của hàm số $g\left( x \right) = f\left( {{x^2} - 2x} \right)$ là:

Đề mẫu ĐGNL HN 2021

Hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^3} - \dfrac{{29}}{8}{x^2} + \dfrac{9}{4}x + \dfrac{3}{8}$, $\forall x\, \in \,\mathbb{R}$. Gọi $S$ là tập hợp các điểm cực tiểu của hàm số $g\left( x \right) = f\left( {2x + 1} \right) - {x^3}.$ Tổng giá trị các phần tử của $S$ bằng

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Phát biểu nào sau đây là sai?

Quan sát đồ thị của hàm số $y = {x^2}$  (H.1.2)

a) Hàm số đồng biến trên khoảng nào?

b) Hàm số nghịch biến trên khoảng nào?

Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:

a) Đồ thị hàm số $y = {x^3} - \frac{3}{2}{x^2}$ (H.1.11);

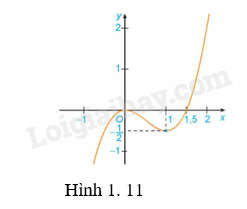
b) Đồ thị hàm số $y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}$ (H.1.12).

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?
A. Nếu $f'\left( x \right) \ge 0$ với mọi x thuộc (a; b) thì hàm số $y = f\left( x \right)$ đồng biến trên (a; b).
B. Nếu $f'\left( x \right) > 0$ với mọi x thuộc (a; b) thì hàm số $y = f\left( x \right)$ đồng biến trên (a; b).
C. Hàm số $y = f\left( x \right)$ đồng biến trên (a; b) khi và chỉ khi $f'\left( x \right) \ge 0$ với mọi x thuộc (a; b).
D. Hàm số $y = f\left( x \right)$ đồng biến trên (a; b) khi và chỉ khi $f'\left( x \right) > 0$ với mọi x thuộc (a; b).

Khoảng nghịch biến của hàm số $y = {x^3} - 6{x^2} + 9x + 1$ là:

A. $\left( { - \infty ;1} \right)$.

B. $\left( {3; + \infty } \right)$.

C. $\left( {1;3} \right)$.

D. $\left( { - \infty ; + \infty } \right)$.

a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập $K \subset \mathbb{R}$, trong đó K là một khoảng, đoạn hoặc nửa khoảng.

b) Cho hàm số $y = f\left( x \right) = {x^2}$ có đồ thị như Hình 2.

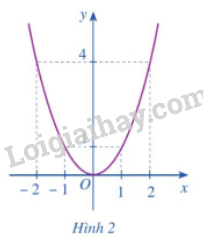
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.

- Xét dấu đạo hàm $f'\left( x \right) = 2x$.

- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số $f\left( x \right) = {x^2}$ và dấu của đạo hàm $f'\left( x \right) = 2x$ trên mỗi khoảng $\left( { - \infty ;0} \right),\left( {0; + \infty } \right)$.

- Hoàn thành bảng biến thiên sau:

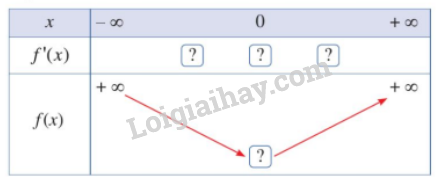
Cho hàm số $y = f\left( x \right)$có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào dưới đây?
A. $\left( {1; + \infty } \right)$.
B. $\left( { - 1;0} \right)$.
C. $\left( { - 1;1} \right)$.
D. $\left( {0;1} \right)$.

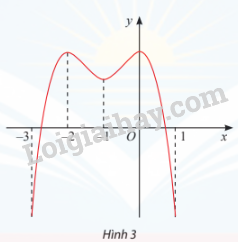
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.

Cho hàm số y=f(x) có đạo hàm trên R và hàm số y=f’(x) có đồ thị như hình 31:

Hàm số y=f(x) đồng biến trên khoảng

a, $\left( { - \infty ;0} \right)$

b, $\left( {0;1} \right)$

c, $\left( {0;2} \right)$

d, $\left( {1;2} \right)$

Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng

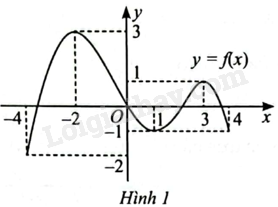
Hàm số $y = f\left( x \right)$ trong Hình 1 nghịch biến trên khoảng nào?

A. $\left( { - 2;1} \right)$.

B. $\left( { - 4; - 2} \right)$.

C. $\left( { - 1;3} \right)$.

D. $\left( {1;3} \right)$.

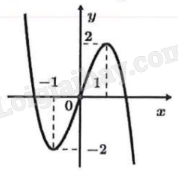
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?

Cho hàm số $f(x) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ dưới đây:

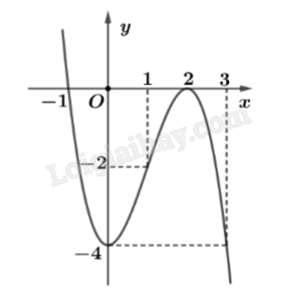
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ dưới đây.

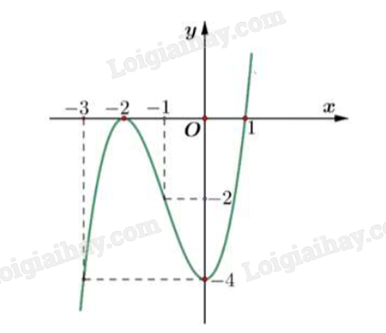
Hàm số y = f(x) đồng biến trên khoảng