Nội dung từ Loigiaihay.Com
1. Một cái lều ở trại hè của học sinh có dạng hình chóp tứ giác đều với chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m và cạnh đáy bằng 2m. Tính diện tích vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp), biết lều này không có đáy.

2. Cho tam giác ANE vuông tại A có đường cao AB.
a) Chứng minh $\Delta ANE\backsim \Delta BEA$.
b) Chứng minh \(A{N^2} = NB.NE\).
c) Cho \(AN = 15cm,NE = 25cm\). Tia phân giác của góc N cắt cạnh AB tại I. Tính NI?
1. Số bạt cần thiết để dựng lều chính là diện tích xung quanh của hình chóp tứ giác đều.
Sử dụng công thức tính diện tích xung quanh của chóp tứ giác đều.
2. a) Chứng minh $\Delta ANE\backsim \Delta BEA$ theo trường hợp góc – góc.
b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{N^2} = NE.NB\).
c) Dựa vào \(A{N^2} = NE.NB\) để tính NB.
Áp dụng định lí Pythagore vào \(\Delta ANB\) để tính AB.
Áp dụng tính chất tia phân giác để tính BI suy ra BI.
Áp dụng định lí Pythagore vào tam giác \(\Delta BIN\) để tính NI.
1.
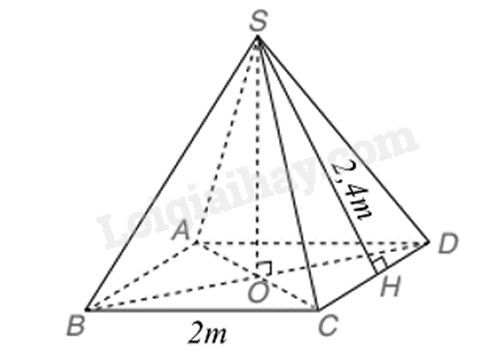
Gọi hình mô tả của cái lều là hình chóp S.ABCD (như hình vẽ).
Diện tích vải lều (diện tích xung quanh của chiếc lều) là:
\({S_{xq}} = \frac{{4.2}}{2}.2,24 = 8,96\left( {{m^2}} \right)\)
Vậy diện tích vải bạt cần thiết để dựng lều là \(8,96{m^2}\).
2.
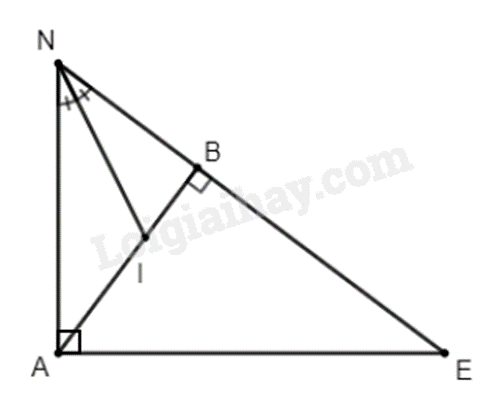
a) Xét \(\Delta ANE\) và \(\Delta BEA\) có:
\(\widehat {NAE} = \widehat {EBA} = {90^0}\)
\(\widehat E\) chung
Suy ra $\Delta ANE\backsim \Delta BEA$ (g.g). (đpcm)
b) Xét \(\Delta ANB\) và \(\Delta ENA\) có:
\(\widehat {ABN} = \widehat {EAN} = {90^0}\)
\(\widehat N\) chung
Suy ra $\Delta ANB\backsim \Delta ENA$ (g.g).
Suy ra \(\frac{{AN}}{{NB}} = \frac{{NE}}{{AN}}\) hay \(A{N^2} = NE.NB\) (đpcm).
c) Thay \(AN = 15cm,NE = 25cm\) vào \(A{N^2} = NE.NB\) (cmt), ta được:
\({15^2} = 25.NB\) suy ra \(NB = \frac{{{{15}^2}}}{{25}} = 9\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác vuông ANB vuông tại B, ta có:
\(A{B^2} = A{N^2} - N{B^2} = {15^2} - {9^2} = 144\) suy ra \(AB = \sqrt {144} = 12\left( {cm} \right)\)
NI là tia phân giác của góc ANB nên ta có:
\(\frac{{AN}}{{NB}} = \frac{{AI}}{{IB}}\) hay \(\frac{{AN}}{{AI}} = \frac{{BN}}{{BI}}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{AN}}{{AI}} = \frac{{BN}}{{BI}} = \frac{{AN + BN}}{{AI + BI}} = \frac{{15 + 9}}{{AB}} = \frac{{24}}{{12}} = 2\)
Suy ra \(BI = \frac{{BN}}{2} = \frac{9}{2} = 4,5\left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác BIN ta có:
\(NI = \sqrt {B{N^2} + B{I^2}} = \sqrt {{9^2} + 4,{5^2}} = \frac{{9\sqrt 5 }}{2}\left( {cm} \right)\)
Vậy \(NI = \frac{{9\sqrt 5 }}{2}cm\).

Các bài tập cùng chuyên đề
Trong các phương trình sau, phương trình bậc nhất một ẩn là
Phương trình nào sau đây nhận \(m = 2\) là nghiệm?
Đường thẳng \(y = 3x + 2023\) tạo với trục Ox một góc như thế nào?
Cho mặt phẳng tọa độ Oxy và điểm A (như hình vẽ).
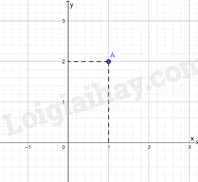
Khi đó tọa độ của điểm A là:
Một hộp có 4 tấm thẻ cùng loại được đánh số lần lượt: 2; 3; 4; 5. Chọn ngẫu nhiên một thẻ từ hộp, kết quả thuận lợi cho biến cố “Số ghi trên thẻ chia hết cho 5” là thẻ
Bạn An gieo một con xúc xắc 50 lần và thống kê kết quả các lần gieo ở bảng sau:

Xác suất thực nghiệm của biến cố “Gieo được mặt số chấm là số nguyên tố” là
Cục Rubik ở hình nào có dạng hình chóp tam giác đều?

Kim tự tháp Louvre (xây dựng vào năm 1988). Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều có chiều cao 21 m, độ dài cạnh đáy là 34 m. Tính thể tích của kim tự tháp Louvre?

Cho hình vẽ
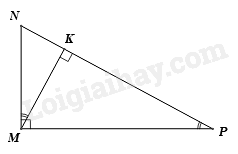
Khi đó các khẳng định sau
(1) $\Delta MKN\backsim \Delta PKM\text{ (g}\text{.g)}$.
(2) $\Delta MKP\backsim \Delta MNP\text{ (g}\text{.g)}$.
Hãy chọn đáp án đúng:
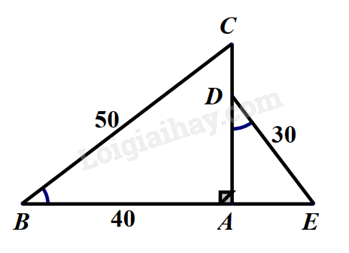
Cho hình vẽ sau, biết \(\widehat B = \widehat D,BC = 50cm,AB = 40cm,DE = 30cm\). Độ dài đoạn thẳng AD là:
Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?
Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:

a) Giải phương trình \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{4} + \frac{1}{2}\).
b) Vẽ đồ thị hàm số y = 2x – 1.
c) Cho hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\). Tìm các hệ số a và b, biết rằng khi x = 0 thì y = 5 và khi x = 2 thì y = 3.
Giải bài toán bằng cách lập phương trình
Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Tỉ lệ học sinh nam của lớp 8A là 60%, tổng số bạn lớp 8A là 40. Ngẫu nhiên gặp 1 thành viên nữ. Tính xác suất thực nghiệm của biến cố “Gặp một học sinh nữ của lớp”?
Cho \({a_1};{a_2};...;{a_{2024}}\) là 2024 số thực thỏa mãn \({a_k} = \frac{{2k + 1}}{{{{\left( {{k^2} + k} \right)}^2}}}\) với \(k \in \left\{ {1;2;...;2024} \right\}\).
Tính tổng \({S_{2024}} = {a_1} + {a_2} + {a_3} + ... + {a_{2024}}\).












