Nội dung từ Loigiaihay.Com
Hàm số nào dưới đây có đồ thị như hình dưới?
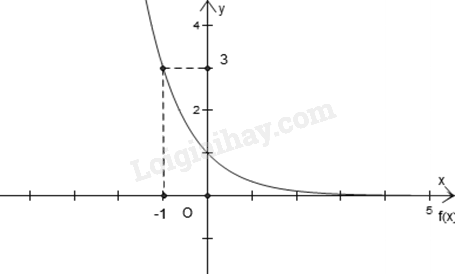
-
A.
y=3x.
-
B.
y=(12)x.
-
C.
y=(13)x.
-
D.
y=(√2)x.
Xét xem đồ thị hàm số nào đi qua điểm (−1;3) và (0;1) thì đó là đồ thị hàm số cần tìm.
Ta thấy đồ thị hàm số y=(13)x đi qua điểm (−1;3) và (0;1) nên hàm số y=(13)x là hàm số cần tìm.
Đáp án : C

Các bài tập cùng chuyên đề
Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
Chọn đáp án đúng.
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:
Chọn đáp án đúng:
Rút gọn biểu thức P=a√5+1.a7−√5(a3+√2)3−√2 (với a>0).
Với giá trị nào của a thì a√8<1a−3?
Chọn đáp án đúng.
logab xác định khi và chỉ khi:
Chọn đáp án đúng.
Khẳng định nào sau đây đúng?
Giá trị của phép tính 4log√23 là:
Chọn đáp án đúng:
Đồ thị hàm số y=ax(a>0,a≠1) cắt trục tung tại điểm có tung độ bằng:
Hàm số y=ax(a>0,a≠1) có tập xác định là:
Hàm số y=log2x đồng biến trên khoảng nào sau đây?
Hàm số nào dưới đây là hàm số mũ?
Cho hàm số f(x)=2x. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn [−2;3]. Khi đó:
Nghiệm của phương trình 2x=9 là:
Nghiệm của phương trình 22x−1=2x là:
Phương trình πx−3=1π có nghiệm là:
Nghiệm của phương trình (116)x+1=642x là:
Tập nghiệm của bất phương trình log23(x−3)≥1 là:












