Chọn đáp án đúng.

\({\log _a}b\) xác định khi và chỉ khi:

Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

Chọn đáp án đúng.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:

Chọn đáp án đúng:

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).

Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

Chọn đáp án đúng.

Khẳng định nào sau đây đúng?

Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:

Chọn đáp án đúng:

Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:

Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?

Hàm số nào dưới đây là hàm số mũ?

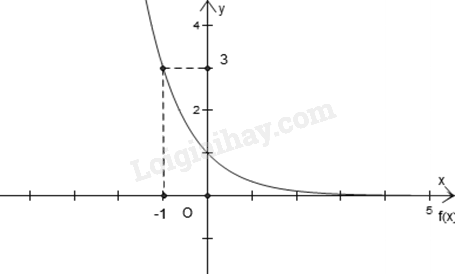
Hàm số nào dưới đây có đồ thị như hình dưới?

Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:

Nghiệm của phương trình \({2^x} = 9\) là:

Nghiệm của phương trình \({2^{2x - 1}} = {2^x}\) là:

Phương trình \({\pi ^{x - 3}} = \frac{1}{\pi }\) có nghiệm là:

Nghiệm của phương trình \({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}}\) là:

Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1\) là: