Nội dung từ Loigiaihay.Com
a) Tìm x biết \(\frac{6}{x} = \frac{{ - 4}}{5}\).
b) Tìm \(x;y\) biết: \(\frac{x}{5} = \frac{y}{3}\) và \(x + 2y = 33\).
c) Tìm a, b, c tỉ lệ với ba số 2; 3; -4 và a + b – c = 18.
a) Dựa vào tính chất của tỉ lệ thức để tìm x.
b, c) Sử dụng tính chất của dãy tỉ số bằng nhau để tìm ẩn.
a) Ta có:
\(\begin{array}{l}\frac{6}{x} = \frac{{ - 4}}{5}\\6.5 = - 4.x\\ - 4x = 30\\x = \frac{{ - 30}}{4} = \frac{{ - 15}}{2}\end{array}\)
Vậy \(x = \frac{{ - 15}}{2}\).
b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{5} = \frac{y}{3} = \frac{{x + 2y}}{{5 + 2.3}} = \frac{{33}}{{11}} = 3\)
Từ đó suy ra:
\(\begin{array}{l}x = 3.5 = 15\\y = 3.3 = 9\end{array}\)
Vậy x = 15; y = 9.
c) Ta có a, b, c tỉ lệ với ba số 2; 3; -4 nên ta có dãy tỉ số bằng nhau:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{{ - 4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{{ - 4}} = \frac{{a + b - c}}{{2 + 3 - \left( { - 4} \right)}} = \frac{{18}}{9} = 2\)
Từ đó suy ra:
\(\begin{array}{l}a = 2.2 = 4\\b = 2.3 = 6\\c = 2.\left( { - 4} \right) = - 8\end{array}\)
Vậy \(a = 4;b = 6;c = - 8\).

Các bài tập cùng chuyên đề
Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}.\) Khẳng định đúng là
Từ đẳng thức \(2.\left( { - 15} \right) = \left( { - 5} \right).6\), ta có thể lập được tỉ lệ thức nào?
Cho \(x,y\) là hai đại lượng tỉ lệ nghịch với nhau, biết \({x_1},{y_1}\) và \({x_2},{y_2}\) là các cặp giá trị tương ứng của chúng. Khẳng định nào sau đây là sai?
Nếu ba số \(a;{\rm{ }}b;{\rm{ }}c\) tương ứng tỉ lệ với \(2;5;7\) ta có dãy tỉ số bằng nhau là:
Cho đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k = - 3.\) Hệ thức liên hệ của \(y\) và \(x\) là:
Biểu thức nào là đa thức một biến?
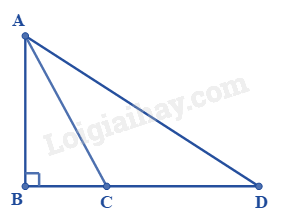
Trong hình vẽ bên, có điểm \(C\) nằm giữa \(B\) và \(D\). So sánh \(AB;AC;AD\) ta được
Trong các bộ ba đoạn thẳng sau đây. Bộ gồm ba đoạn thẳng nào là độ dài ba cạnh của một tam giác?
Cho đại lượng y tỉ lệ thuận với đại lượng x. Khi \(x = 4\) thì \(y = 16\) . Vậy hệ số tỉ lệ bằng
Biểu thức biểu thị chu vi của hình chữ nhật có chiều dài \(8cm\) và chiều rộng \(6cm\) là
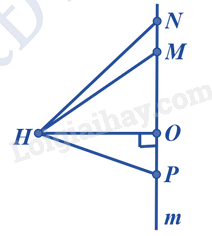
Đường vuông góc kẻ từ H xuống đường thẳng m là:
Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22. Tính số học sinh của mỗi lớp, biết rằng lớp 7C có nhiều hơn lớp 7A là 2 học sinh.
Một khu đất hình chữ nhật có chiều dài và chiều rộng tỉ lệ với 8 và 5. Diện tích khu đất đó bằng \(360{m^2}\). Tính chiều dài và chiều rộng của khu đất đó.
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:
a) BH = CH.
b) BA > BM.
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng \(AB + AC > 2AM\).












