Nội dung từ Loigiaihay.Com
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng AB+AC>2AM.
Dựa vào kiến thức về đường trung tuyến trong tam giác.
Lấy điểm D thuộc tia đối của tia MA sao cho AM = DM.
Chứng minh ΔAMB=ΔDMC suy ra AB=CD.
Sử dụng bất đẳng thức tam giác để chứng minh AB+AC>AD=2AM.
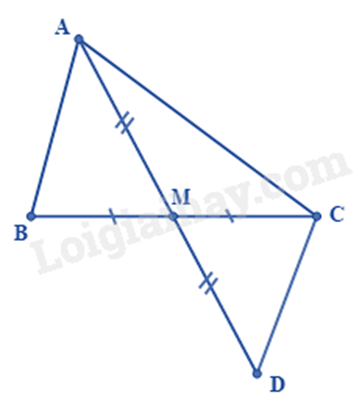
Do AM là trung tuyến của tam giác ABC nên ta có BM = CM.
Trên tia đối của tia MA lấy điểm D sao cho AM = DM.
Xét ΔAMB và ΔDMC có:
AM=DM
BM=CM
^AMB=^DMC (hai góc đối đỉnh)
Suy ra ΔAMB=ΔDMC (c.g.c) suy ra AB = CD (hai cạnh tương ứng)
Khi đó AB+AC=DC+AC>AD (bất đẳng thức tam giác)
Mà AM = DM nên AD = 2.AM
Do đó: AB+AC>2AM.

Các bài tập cùng chuyên đề
Bài 1 :
Cho ΔABC cân tại A có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 17cm.
-
A.
BC=7cm hoặc BC=5cm.
-
B.
BC=7cm
-
C.
BC=5cm.
-
D.
BC=6cm.
Bài 2 :
Bộ ba số nào là độ dài ba cạnh của một tam giác?
-
A.
4cm,5cm,10cm.
-
B.
5cm,5cm,12cm.
-
C.
11cm,11cm,20cm.
-
D.
9cm,20cm,11cm.
Bài 3 :
Cho hai bộ ba thanh tre nhỏ có độ dài như sau:
Bộ thứ nhất: 10 cm, 20 cm, 25 cm.
Bộ thứ hai: 5 cm, 15 cm, 25 cm.
Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.
Bài 4 :
Với bộ ba thanh tre ghép lại được thành một tam giác trong HĐ1, em hãy so sánh độ dài của thanh tre bất kì với tổng độ dài 2 thanh còn lại
Bài 5 :
Ý kiến của em thì sao?
Bài 6 :
Hỏi ba độ dài nào sau đây không thể là độ dài ba cạnh của một tam giác? Vì sao? Hãy vẽ tam giác nhận ba độ dài còn lại làm độ dài 3 cạnh.
a) 5 cm, 4 cm, 6 cm.
b) 3 cm, 6 cm, 10 cm.
Bài 7 :
Trở lại tình huống mở đầu, em hãy giải thích vì sao nếu dựng cột điện ở vị trí C trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất? (H.9.17)
Bài 8 :
Cho các bộ ba đoạn thẳng có độ dài như sau:
a) 2 cm, 3 cm, 5 cm
b) 3 cm, 4 cm, 6 cm
c) 2 cm, 4 cm, 5 cm.
Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Bài 9 :
a) Cho tam giác ABC có AB = 1 cm, BC = 7 cm. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).
b) Cho tam giác ABC có AB= 2 cm, BC = 6 cm và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).
Bài 10 :
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
Bài 11 :
Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao?
Bài 12 :
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2 cm và 5 cm.
Bài 13 :
Độ dài hai cạnh của một tam giác bằng 7 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của nó theo xentimet là một số tự nhiên lẻ.
Bài 14 :
Biết rằng hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a+b).
Bài 15 :
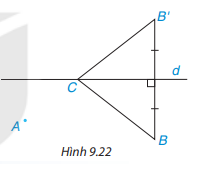
Hai khu vườn A và B nằm về một phía của con kênh d. Hãy xác định bên bờ kênh cùng phía với A và B, một điểm C để đặt máy bơm nước từ kênh tưới cho hai khu vườn sao cho tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất.
Bài 16 :
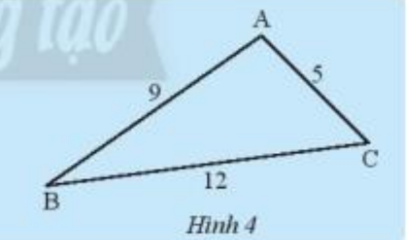
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
Bài 17 :
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 7cm; 8cm; 11cm
b) 7cm; 9cm; 16cm
c) 8cm; 9cm; 16cm
Bài 18 :
Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?
Bài 19 :
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 4cm; 5cm; 7cm
b) 2cm; 4cm; 6cm
c) 3cm; 4cm; 8cm
Bài 20 :
Trong một trường học, người ta bắt đầu đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15m, AB = 45m
a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?
b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.
Bài 21 :
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
-
A.
5cm;4cm;1cm;
-
B.
3cm;4cm;5cm;
-
C.
5cm;2cm;2cm;
-
D.
1cm;4cm;10cm;
Bài 22 :
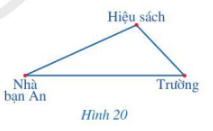
Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?
Bài 23 :
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có AB=3cm, BC=2cm, AC=4cm.
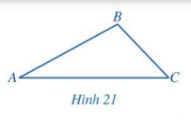
a) Hãy sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại số đo độ dài ba cạnh của tam giác ABC mà bạn Thảo đã nói.
b) So sánh AB+BCvà AC.
Bài 24 :
Cho tam giác ABC có AB=2cm, BC=4cm. So sánh hai cạnh AC và AB.
Bài 25 :
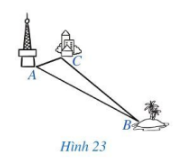
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ kín đến bán kính 100 km.
Người ta đặt một trạm phát sóng 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 20 km (Hình 23). Sóng 4G của trạm phát sóng A có thể phủ đến đảo đó được không? Vì sao?
Bài 26 :
Có hay không một tam giác mà độ dài ba cạnh của tam giác đó được cho bởi các độ dài trong mỗi trường hợp sau?
a) 8 cm, 5 cm, 3 cm;
b) 12 cm, 6 cm, 6 cm;
c) 15 cm, 9 cm, 4 cm.
Bài 27 :
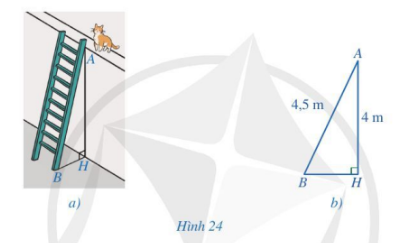
Con mèo của bạn Huê bị mắc kẹt trên gờ tường cao 4 m. Bác bảo vệ sử dụng một cái thang để đưa mèo xuống giúp bạn Huê. Bác đặt thang dựa vào gờ tường (Hình 24a), khoảng cách từ chân thang đến điểm chạm vào gờ tường là AB=4,5m. Hình 24b mô tả hình ảnh chiếc thang dựa vào tường trong Hình 24a. Bạn Huê khẳng định chân thang cách chân tường là BH=0,5m. Khẳng định của bạn Huê có đúng không? Vì sao?
Bài 28 :
Có hai xã cùng ở một bên bờ sông Lam. Các kĩ sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã. Để thuận lợi cho người dân đi lại, các kĩ sư cần phải chọn vị trí của cây cầu sao cho tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất. Bạn Nam đề xuất cách xác định vị trí của cây cầu như sau (Hình 54):
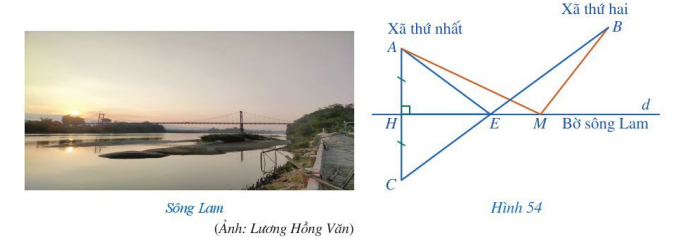
- Kí hiệu điểm A chỉ vị trí xã thứ nhất, điểm B chỉ vị trí xã thứ hai, đường thẳng d chỉ vị trí bờ sông Lam.
- Kẻ AH vuông góc với d (H thuộc d), kéo dài AH về phía H và lấy C sao cho AH = HC.
- Nối C với B, CB cắt đường thẳng d tại E.
Khi đó, E là vị trí của cây cầu.
Bạn Nam nói rằng: Lấy một điểm M trên đường thẳng d, M khác E thì
MA + MB > EA + EB
Em hãy cho biết bạn Nam nói đúng hay sai. Vì sao?
Bài 29 :
Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ hai đi từ B đến A (Hình 141). Theo em, đường nào đi dài hơn? Vì sao?
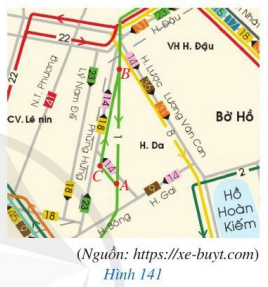
Bài 30 :
Cho tam giác MNP có MN = 1 dm, NP = 2 dm, MP = x dm với x∈{1;2;3;4}. Khi đó, x nhận giá trị nào?
A. 1.
B. 2.
C. 3.
D. 4.