Để đổi từ độ F (Fahrenheit) sang độ C (Celcius) ta dùng công thức sau:

\(C = \frac{5}{9}\left( {F - 32} \right)\).

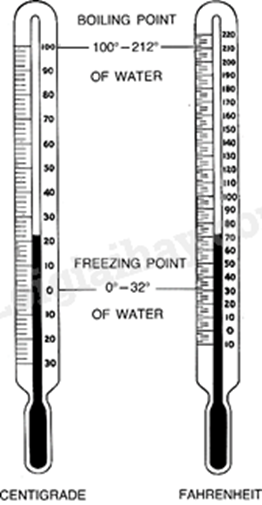
a) C có phải là hàm số bậc nhất theo biến số F không? Giải thích.

b) Hãy tính C khi F = 30; F = 80

c) Hãy tính F khi C = -10

Cho hàm số \(y = f\left( x \right) = \frac{1}{2}x + 5\), giá trị \(f\left( 0 \right)\) là:

Cho \(y = \left( {m - 3} \right)x + 7\),  hàm số không phải là hàm bậc nhất khi m bằng:

Cho\(y = \left( {m + 3} \right)x - 2\), giá trị của m để hàm số có hệ số góc âm trên \(\mathbb{R}\) là:

Góc tạo bởi đường thẳng  \(y =  - x + 5\) và trục Ox là:

Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.

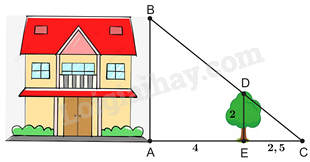
Khi đó chiều cao AB của ngôi nhà là:

Cho hình vẽ:

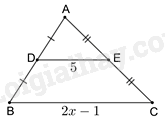
Giá trị của x là:

Cho hình vẽ:

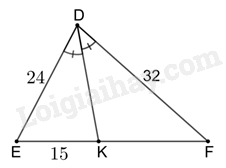
Độ dài KF là:

Cho \(\left( {{d_1}} \right):y = \frac{{m - 1}}{2}x - m - 5\) và \(\left( {{d_2}} \right):y = \left( {m + 3} \right)x - 2m + 7\)

a) Tìm m để \(\left( {{d_1}} \right)//\left( {{d_2}} \right)\).

b) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một hệ trục với giá trị m vừa tìm được.

Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

Cho hình thang MNPQ (MN // PQ), đường cao ME. Hình thang MNPQ có diện tích 36cm, MN = 4cm, PQ = 8cm. Gọi I là giao điểm của hai đường chéo MP và NQ.

a) Tính ME.

b) Chứng minh \(IP = \frac{2}{3}MP\).

c) Tính diện tích tam giác IPQ.

Tìm các giá trị nguyên của m để hai đường thẳng d: y = mx -2; d’: y = 2x + 1 cắt nhau tại điểm có hoành độ là số nguyên?