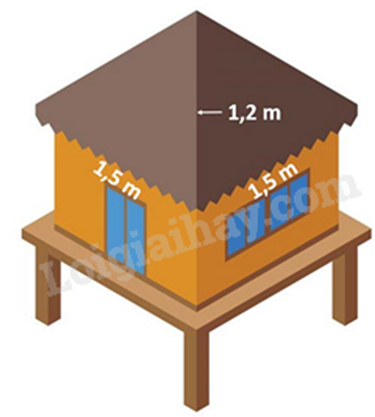
1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)

2. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB < AC\). Gọi \(M\) là trung điểm của \(BC\), kẻ \(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\).

a) Chứng minh \(AM = DE\).

b) Chứng minh tứ giác \(DMCE\) là hình bình hành.

c) Gọi \(AH\) là đường cao của tam giác \(ABC\) (\(H \in BC\)). Chứng minh tứ giác \(DHME\) là hình thang cân.

1. 

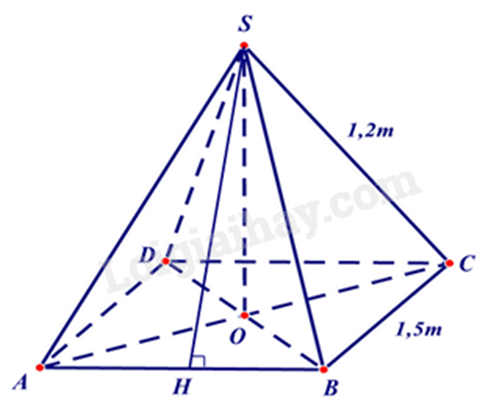
Ta có hình vẽ minh họa cho mái nhà của chòi như hình trên.

Gọi SH là đường cao của tam giác SAB nên SH là trung đoạn của hình chóp S.ABCD.

Vì S.ABCD là hình chóp tứ giác đều nên SAB là tam giác cân. Do đó SA = SB = 1,2m. Khi đó SH là đường cao đồng thời là đường trung tuyến nên AH = BH = \(\frac{1}{2}\) AB = \(\frac{1}{2}\).1,5 = 0,75(m).

Áp dụng định lí Pythagore vào tam giác vuông SHB, ta có:

\(SH = \sqrt {S{B^2} - B{H^2}}  = \sqrt {1,{2^2} - 0,{{75}^2}}  \approx 1\left( m \right)\)

Diện tích vải bạc cần dùng để phủ mái chòi chính là diện tích xung quanh của hình chóp tứ giác đó.

Diện tích xung quanh của hình chóp là:

\({S_{xq}} = \frac{{4.1,5}}{2}.1 = 3\left( {{m^2}} \right)\).

Vậy diện tích vải bạc cần dùng để phủ mái chòi là 3m².

2. 

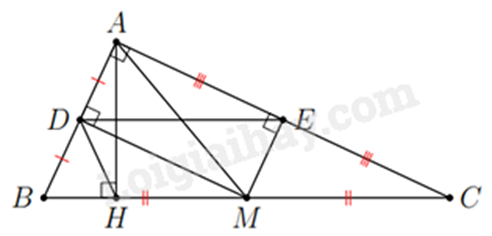
a) Xét tứ giác ADME có:

\(\widehat A = {90^0}\) (tam giác ABC vuông tại A)

\(\widehat D = \widehat E = {90^0}\) (\(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\))

=> ADME là hình chữ nhật (tứ giác có 3 góc vuông).

b) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC nên AM = MC = \(\frac{1}{2}\)

Khi đó tam giác AMC cân tại M. Mà ME vuông góc với AC nên ME là đường cao đồng thời là đường trung tuyến của tam giác AMC suy ra E là trung điểm của AC \( \Rightarrow \) AE = EC. (1)

ADME là hình chữ nhật nên DM // AE và DM = AE (2)

Từ (1) và (2) suy ra DM // EC và DM = EC, do đó tứ giác DMCE là hình bình hành.

c) DMCE là hình bình hành nên DE // MC => DE // HM (H thuộc đường thẳng CM)

=> DHME là hình thang.

Xét tam giác AMB có AM = BM nên tam giác AMB cân tại M. Mà MD vuông góc với AB nên MD đường cao đồng thời là đường trung tuyến của tam giác ABM suy ra D là trung điểm của AB.

Xét tam giác ABH vuông tại H, D là trung điểm của AB nên HD là đường trung tuyến ứng với cạnh huyền của tam giác AHB => \(HD = AD = \frac{1}{2}AB\).

Mà ADME là hình chữ nhật nên AD = ME suy ra HD = ME.

Hình thang DHME có HD = ME nên DHME là hình thang cân.