Nội dung từ Loigiaihay.Com
Đề bài
Cho phân thức: \(A = \frac{{1 - 2x}}{{1 - 4{x^2}}}\)
a) Với điều kiện nào của x thì giá trị của phân thức A được xác định?
b) Rút gọn phân thức A.
c) Tính giá trị nguyên của x để phân thức A có giá trị nguyên.
Phương pháp giải
a) Điều kiện để phân thức A xác định là mẫu thức khác 0.
b) Phân tích mẫu thức thành nhân tử để rút gọn.
c) Để phân thức A nguyên thì tử thức phải chia hết cho mẫu thức.
Lời giải của GV HocTot.Nam.Name.Vn
a) Phân thức A xác định khi và chỉ khi \(1 - 4{x^2} \ne 0 \Leftrightarrow \left( {1 - 2x} \right)\left( {1 + 2x} \right) \ne 0 \Leftrightarrow \left[ \begin{array}{l}1 - 2x \ne 0\\1 + 2x \ne 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ne \frac{1}{2}\\x \ne - \frac{1}{2}\end{array} \right.\)
b) Ta có:
\(A = \frac{{1 - 2x}}{{1 - 4{x^2}}} = \frac{{\left( {1 - 2x} \right)}}{{\left( {1 - 2x} \right)\left( {1 + 2x} \right)}} = \frac{1}{{1 + 2x}}\)
c) Phân thức A có giá trị nguyên khi và chỉ khi \(\frac{1}{{1 + 2x}}\) nguyên, hay \(\left( {1 + 2x} \right) \in U\left( 1 \right) = \left\{ { \pm 1} \right\}\).
Ta có bảng giá trị sau:
|
1 + 2x |
-1 |
1 |
|
x |
-1 (TM) |
0 (TM) |
|
\(A = \frac{1}{{1 + 2x}}\) |
-1 |
1 |
Vậy \(x \in \left\{ { - 1;0} \right\}\) thì phân thức A có giá trị nguyên.
Các bài tập cùng chuyên đề
Bài 1 :
Giá trị của biểu thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi x = -2 là:
Xem lời giải >>
Bài 2 :
Hiệu của biểu thức \(\frac{{{\rm{x\;}} + {\rm{\;}}1{\rm{\;}}}}{{{\rm{x\;}} - {\rm{\;}}1{\rm{\;}}}}\) \(-\) \(\frac{{{\rm{x\;}}-\;4}}{{{\rm{x\;}}-{\rm{\;}}1}}\) bằng:
Xem lời giải >>
Bài 3 :
Cho \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{P}{{{x^2} - {y^2}}}\). Đa thức P là:
Xem lời giải >>
Bài 4 :
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích xung quanh của hình chóp.
Xem lời giải >>
Bài 5 :
Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm3; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là (Làm tròn đến hàng đơn vị)
Xem lời giải >>
Bài 6 :
Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Xem lời giải >>
Bài 7 :
Hình bình hành ABCD là hình chữ nhật khi:
Xem lời giải >>
Bài 8 :
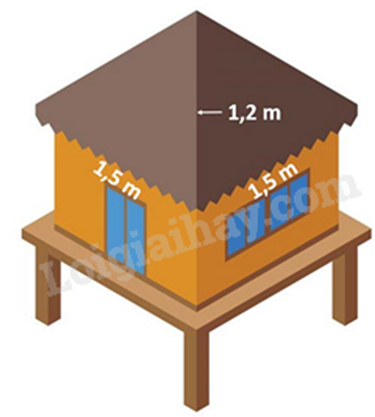
1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)
2. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB < AC\). Gọi \(M\) là trung điểm của \(BC\), kẻ \(MD\) vuông góc với \(AB\) tại \(D\), \(ME\) vuông góc với \(AC\) tại \(E\).
a) Chứng minh \(AM = DE\).
b) Chứng minh tứ giác \(DMCE\) là hình bình hành.
c) Gọi \(AH\) là đường cao của tam giác \(ABC\) (\(H \in BC\)). Chứng minh tứ giác \(DHME\) là hình thang cân.
Xem lời giải >>