Nội dung từ Loigiaihay.Com
Cho đoạn thẳng \(AB,O\) là trung điểm của \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ các tia \(Ax;By\) vuông góc với \(AB.\) Gọi \(C\) là một điểm thuộc tia \(Ax.\) Đường vuông góc với \(OC\) tại ${\rm{O}}$ cắt tia \(By\) ở \(D.\) Khi đó
-
A.
\(BD = CD + AC\)
-
B.
\(AC = DC + BD\)
-
C.
\(CD = AC - BD\)
-
D.
\(CD = AC + BD\)
+ Kéo dài \(OC\) cắt \(BD\) tại \(K.\)
+ Chứng minh \(AC = BK\) dựa vào hai tam giác bằng nhau \(AOC\) và \(BOK.\)
+ Chứng minh hai tam giác bằng nhau \(COD\) và \(KOD\) từ đó suy mối quan hệ giữa các đoạn thẳng.
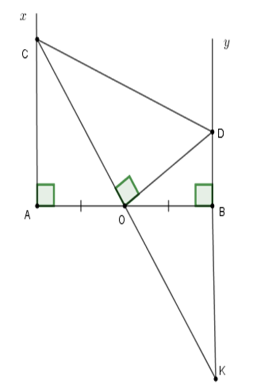
Kéo dài \(OC\) cắt \(BD\) tại \(K.\) Khi đó \(OD \bot OC \Rightarrow OD \bot CK \Rightarrow \widehat {COD} = \widehat {KOD} = 90^\circ \) ; \(AB \bot DK \Rightarrow \widehat {OBD} = \widehat {OBK} = 90^\circ .\)
Xét tam giác \(AOC\) và tam giác \(BOK\) có
+ \(\widehat {OAC} = \widehat {OBK} = 90^\circ \)
+ \(OA = OB\,\) (\(O\) là trung điểm của \(AB\))
+ \(\widehat {AOC} = \widehat {BOK}\) (hai góc đối đỉnh)
Suy ra \(\Delta AOC = \Delta BOK\left( {g - c - g} \right)\) \( \Rightarrow OC = OK\) (hai cạnh tương ứng); \(AC = BK\) (hai cạnh tương ứng)
Xét tam giác \(DOC\) và tam giác \(DOK\) có
+ \(OC = OK\) (cmt)
+ \(\widehat {DOC} = \widehat {DOK} = 90^\circ \)
+ Cạnh \(OD\) chung,
Suy ra \(\Delta DOC = \Delta DOK\left( {g - c - g} \right)\) \( \Rightarrow CD = DK\) (hai cạnh tương ứng)
Ta có $DK = DB + BK$ mà \(AC = BK\)(cmt) và \(CD = DK\) (cmt) nên \(CD = AC + BD.\)
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P\). Cần thêm một điều kiện gì để tam giác $MPN$ và tam giác $CBA$ bằng nhau theo trường hợp góc – cạnh – góc ?
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điểu kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc:
Cho tam giác $ABC$ và tam giác $MNP$ có $\widehat B = \widehat N = {90^ \circ }$, $AC = MP,$ \(\widehat C = \widehat M\) . Phát biểu nào trong các phát biểu sau đây là đúng:
Cho góc nhọn $xOy,Oz$ là tia phân giác của góc đó. Qua điểm $A$ thuộc tia $Ox$ kẻ đường thẳng song song với $Oy$ cắt $Oz$ ở $M.$ Qua $M$ kẻ đường thẳng song song với $Ox$ cắt $Oy$ ở $B.$ Chọn câu đúng.
Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.
Cho tam giác $DEF$ và tam giác $HKG$ có \(\widehat D = \widehat H\), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc $G$ là:
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE,$ \(\widehat B = \widehat E\) , \(\widehat A = \widehat D\). Biết $AC = 6cm.$ Độ dài $DF$ là:
Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.
Cho tam giác $ABC,D$ là trung điểm của $AB.$ Đường thẳng qua $D$ và song song với $BC$ cắt $AC$ ở $E,$ đường thẳng qua $E$ và song song với $AB$ cắt $BC$ ở $F.$ Khi đó
Cho tam giác \(ABC\) có \(\widehat A = {60^0}.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D,\) tia phân giác của góc \(C\) cắt \(AB\) ở \(E.\) Các tia phân giác đó cắt nhau ở \(I.\) Tính độ dài \(ID,\) biết \(IE = 2cm.\)
Cho hai đoạn thẳng \(AB,CD\) song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song \(AC,BD\). Chọn câu đúng:












