Nội dung từ Loigiaihay.Com
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)
-
A.
\({30^0}\)
-
B.
\({45^0}\)
-
C.
\({60^0}\)
-
D.
\({90^0}\).
Áp dụng tính chất tam giác vuông cân, tính chất đường cao của tam giác.
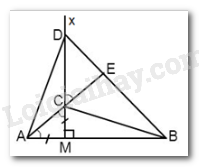
Vì $Mx \bot AB \Rightarrow \widehat {AMx} = {90^0}$
Xét $\Delta AMC$ có $\left\{ \begin{array}{l}\widehat {AMC} = {90^0}\left( {cmt} \right)\\MA = MC\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MAC} = \widehat {MCA} = {45^0}$ (tính chất tam giác vuông cân)
Do đó \(\widehat {DCE} = \widehat {MCA} = {45^0}\) (đối đỉnh)
Xét $\Delta BMD$ có: $\left\{ \begin{array}{l}\widehat {BMD} = {90^0}\left( {cmt} \right)\\MB = MD\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MBD} = \widehat {MDB} = {45^0}$(tính chất tam giác vuông cân)
Xét $\Delta CDE$ có: \(\widehat {CDE} = \widehat {DCE} = {45^0} \) \(\Rightarrow \widehat {CDE} + \widehat {DCE} = {90^0} \Rightarrow \widehat {DEC} = {90^0}.\)
Lại có: \(\widehat {DEC} + \widehat {AEB} = {180^0}\) (kề bù) \( \Rightarrow \widehat {AEB} = {180^0} - \widehat {DEC} = {180^0} - {90^0} = {90^0}\) .
Đáp án : D

Các bài tập cùng chuyên đề
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\) là tam giác gì?
Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.












