Nội dung từ Loigiaihay.Com
Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.
-
A.
\(AB + AC > HA + HB + HC\)
-
B.
\(AB + AC < HA + HB + HC\)
-
C.
\(AB + AC = HA + HB + HC\)
-
D.
\(AB + AC \le HA + HB + HC\)
- Qua \(H\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(F\), kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E\).
- Chứng minh \(\Delta AEH = \Delta HFA\,\)\( \Rightarrow EH = AF;\,AE = HF\) (hai cạnh tương ứng).
- Sử dụng quan hệ đường xiên – đường vuông góc để chứng minh \(BF > BH\),\(CE > CH\).
- Áp dụng bất đẳng thức tam giác vào \(\Delta AEH\) ta có: \(AE + EH > HA\).
Từ đó lập luận suy ra điều phải chứng minh.
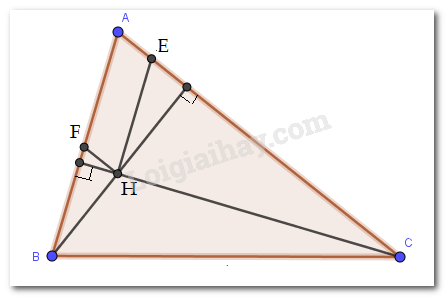
Qua \(H\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(F\), kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E\).
Vì \(AE//HF\) (cách vẽ) nên \(\widehat {EAH} = \widehat {FHA}\) (hai góc so le trong bằng nhau)
Vì \(AF//HE\) (cách vẽ) nên \(\widehat {AHE} = \widehat {HAF}\) (hai góc so le trong bằng nhau)
Xét \(\Delta AEH\) và \(\Delta HFA\) có:
\(AH\) cạnh chung
\(\widehat {EAH} = \widehat {FHA}\,\,(cmt)\)
\(\widehat {AHE} = \widehat {HAF}\,\,(cmt)\)
\( \Rightarrow \Delta AEH = \Delta HFA\,(g.c.g)\)
\( \Rightarrow EH = AF;\,AE = HF\) (hai cạnh tương ứng).
Vì \(BH \bot AC\) và \(FH//AC\) nên \(BH \bot FH\).
Ta có: \(BF;\,BH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(B\) đến \(FH\) nên \(BF > BH\) (quan hệ đường xiên – đường vuông góc).
Vì \(CH \bot AB\) và \(EH//AB\) nên \(CH \bot EH\).
Ta có: \(CE;\,CH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(C\) đến \(EH\) nên \(CE > CH\) (quan hệ đường xiên – đường vuông góc).
Xét \(\Delta AEH\) có: \(AE + EH > HA\) (bất đẳng thức tam giác)
Ta có: \(AB + AC = AF + FB + AE + EC\)
\( \Rightarrow AB + AC = EH + FB + AE + EC\) (vì \(AF = EH\,(cmt)\))
\( \Rightarrow AB + AC = \left( {AE + EH} \right) + FB + EC > HA + HB + HC\).
Vậy \(AB + AC > HA + HB + HC\).
Đáp án : A

Các bài tập cùng chuyên đề
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\) là tam giác gì?
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)












