Nội dung từ Loigiaihay.Com
Cho tam giác $MNP,$ hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O.$ Tính diện tích tam giác $MNP,$ biết diện tích tam giác $MNO$ là \(12c{m^2}\).
-
A.
$18\,c{m^2}$
-
B.
\(48\,c{m^2}\)
-
C.
\(36\,c{m^2}\)
-
D.
\(24\,c{m^2}\)
+) Dựa vào đinh lý về tính chất ba đường trung tuyến của một tam giác để tìm mối liên hệ giữa các cạnh.
+) Áp dụng công thức tính diện tích của một tam giác.
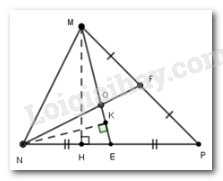
Gọi $MH$ là đường cao kẻ từ $M$ xuống cạnh $BC,NK$ là đường cao kẻ từ $N$ xuống cạnh $ME.$
Hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O$ nên $O$ là trọng tâm tam giác $MNP,$ do đó \(MO = \dfrac{2}{3}ME\).
Có $ME$ là đường trung tuyến ứng với cạnh $NP$ nên $E$ là trung điểm của $NP,$ suy ra $NP = 2.NE$
Ta có:
\(\dfrac{{{S_{MNO}}}}{{{S_{MNE}}}} = \dfrac{{\dfrac{1}{2}.NK.MO}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{{\dfrac{1}{2}.NK.\dfrac{2}{3}.ME}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{2}{3}\) \(\Rightarrow {S_{MNO}} = \dfrac{2}{3}{S_{MNE}}\)
\(\dfrac{{{S_{MNE}}}}{{{S_{MNP}}}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.NP}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.2.NE}} = \dfrac{1}{2}\) \( \Rightarrow {S_{MNE}} = \dfrac{1}{2}{S_{MNP}}\)
\(\Rightarrow {S_{MNP}} = 2.{S_{MNE}} = 3.{S_{MNO}}\) \( \Rightarrow {S_{MNP}} = 3.12 = 36\,c{m^2}\)
Đáp án : C

Các bài tập cùng chuyên đề
Chọn câu sai.
Tam giác \(ABC\) có trung tuyến \(AM = 12\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
Cho tam giác \(ABC\) có hai đường trung tuyến \(BD;CE\) sao cho \(BD = CE\). Khi đó tam giác \(ABC\)
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.












