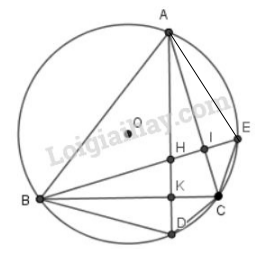
Bài 95 trang 105 SGK Toán 9 tập 2Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Đề bài Các đường cao hạ từ \(A\) và \(B\) của tam giác \(ABC\) cắt nhau tại \(H\) (góc \(C\) khác \(90^0\)) và cắt đường tròn ngoại tiếp tam giác \(ABC\) lần lượt tại \(D\) và \(E\). Chứng minh rằng: a) \(CD = CE\) ; b) \(ΔBHD\) cân ; c) \(CD = CH\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Sử dụng: “Hai góc nội tiếp cùng chắn một cung thì bằng nhau” và hai góc phụ nhau từ đó suy ra hai cung bằng nhau và hai dây bằng nhau. b) Chứng minh tam giác BHD có BK vừa là đường cao vừa là đường phân giác nên nó là tam giác cân c) Sử dụng tính chất đường trung trực của đoạn thẳng Lời giải chi tiết
a) Gọi K là giao điểm của BC và AD Gọi I là giao điểm của BE và AC Cách 1: Ta có: \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}B}\) (1) (2 góc nội tiếp cùng chắn cung \(AB\)) \(\widehat {DBC} + \widehat {ADB} = {90^0}\) (2) (do tam giác BDK vuông tại K) \(\widehat {AEB} + \widehat {CAE} = {90^0}\) (3) (do tam giác AIE vuông tại I) Từ (1), (2), (3) \( \Rightarrow \widehat {CB{\rm{D}}} = \widehat {CA{\rm{E}}}\) (cùng phụ với hai góc bằng nhau) Có \(\widehat {CBD}\) là góc nội tiếp chắn cung CD \(\widehat {EAC}\) là góc nội tiếp chắn cung CE ⇒ \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\) Suy ra \(CD = CE\) Cách 2: Vì \(BC \bot AD\) nên \(\widehat{AKB}=90^0\) Lại có \(\widehat{AKB}\) là góc có đỉnh bên trong đường tròn chắn cung AB và CD nên \(\widehat{AKC}=\dfrac{sđ\overparen {DC}+sđ \overparen {BA}}{2}=90^0\) Suy ra \(sđ\overparen {AB}+sđ \overparen {CD}=180^0\) (1) Vì \(BE \bot AC\) nên \(\widehat{AIB}=90^0\) Lại có \(\widehat{AIB}\) là góc có đỉnh bên trong đường tròn chắn cung AB và CE nên \(\widehat{AIB}=\dfrac{sđ\overparen {CE}+sđ \overparen {AB}}{2}=90^0\) Suy ra \(sđ\overparen {AB}+sđ \overparen {CE}=180^0\) (2) Từ (1) và (2) suy ra \(sđ \overparen {CE}=sđ \overparen {CD}\) Suy ra \( \overparen {CE}=\overparen {CD}\), do đó \(CE=CD.\) b) Ta có \(\widehat {EBC}\) và \(\widehat {CB{\rm{D}}}\) là góc nội tiếp lần lượt chắn cung \(\overparen{CE}\) và \(\overparen{CD}\) trong đường tròn \(O\) và \(\overparen{CD}\)= \(\overparen{CE}\) nên \(\widehat {EBC} = \widehat {CB{\rm{D}}}\) ( 2 góc nội tiếp chắn 2 cung bằng nhau thì bằng nhau) \(\Rightarrow\) BK là phân giác của \(\widehat {HBD}\) Lại có BK vuông góc với HD (giả thiết H là trực tâm của tam giác ABC). Suy ra BK vừa là đường cao vừa là đường phân giác của tam giác HBD nên \(∆BHD\) cân tại \(B\) c) Vì \(∆BHD\) cân nên đường cao \(BK\) đồng thời là đường trung trực. Điểm \(C\) nằm trên đường trung trực của \(HD\) nên \(CH = CD\)
|