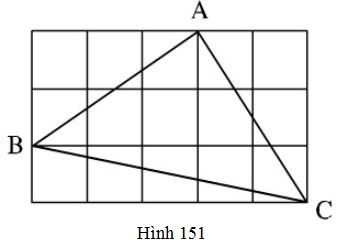
Bài 71 trang 141 SGK Toán 7 tập 1

Đề bài

Tam giác $ABC$ trên giấy kẻ ô vuông (h.151) là tam giác gì ? Vì sao ?

Lời giải chi tiết

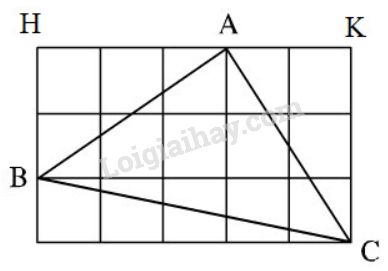
Gọi tên như hình vẽ. 

Xét $∆AHB$ và $∆CKA$ có:

$AH = CK$ ($= 3$ ô vuông)

$\widehat H = \widehat K\left( { = {{90}^o}} \right)$

$HB = KA$ ($= 2$ ô vuông)

$\Rightarrow  ∆AHB = ∆CKA$ (c.g.c)

$\Rightarrow AB = CA$ (hai cạnh tương ứng)

$\Rightarrow \widehat {BAH} = \widehat {ACK}$ (hai góc tương ứng).

Ta lại có: $\widehat {ACK} + \widehat {CAK} = {90^o}$ (hai góc nhọn của tam giác vuông phụ nhau).

Nên $\widehat {BAH} + \widehat {CAK} = {90^0}$

Do đó $\widehat {BAC} = 180^o - (\widehat {BAH} + \widehat {CAK})$$= 180^o - 90^0 = 90^o$

Vậy tam giác $ABC$ là tam giác vuông cân tại $A.$

Cách khác:

Gọi độ dài cạnh của mỗi ô vuông là $1$. Áp dụng định lí Pytago vào các tam giác vuông, ta có:

$\begin{array}{l} A{B^2} = {2^2} + {3^2} = 13\\ A{C^2} = {2^2} + {3^2} = 13\\ B{C^2} = {5^2} + {1^2} = 26 \end{array}$

Ta có $A{B^2} + A{C^2} = 13 + 13 = 26 = B{C^2}$ nên $\Delta ABC$ vuông tại $A$ (theo định lí Pytago đảo).

Lại có $AB^2=AC^2(=13)$ nên $AB=AC$

Vậy $\Delta ABC$ vuông cân tại $A$.

HocTot.Nam.Name.Vn