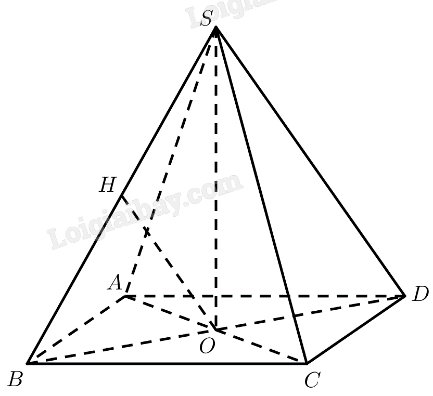
Bài 7 trang 82 SGK Toán 11 tập 2 – Chân trời sáng tạo

Đề bài

Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh đều bằng $a$ và có $O$ là giao điểm hai đường chéo của đáy.

a) Tính khoảng cách giữa hai đường thẳng $AC$ và $SB$.

b) Tinh thể tích của khối chóp.

Lời giải chi tiết

 

a) Kẻ $OH \bot SB\left( {H \in SB} \right)$

$S.ABC{\rm{D}}$ là chóp tứ giác đều $\Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC$

$ABC{\rm{D}}$ là hình vuông $\Rightarrow AC \bot B{\rm{D}}$

$\Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH$

Mà $OH \bot SB$

$\Rightarrow d\left( {AC,SB} \right) = OH$

$B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}}  = a\sqrt 2  \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}$

$\Delta SBO$ vuông tại $O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}}  = \frac{{a\sqrt 2 }}{2}$

$\Delta SBO$ vuông cân tại $O$ có đường cao $OH$

$\Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}$

b) ${S_{ABC{\rm{D}}}} = A{B^2} = {a^2}$

${V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}$