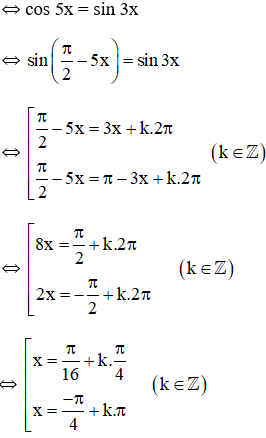Giải bài 7 trang 29 SGK Đại số và Giải tích 11Giải các phương trình sau: Video hướng dẫn giải Giải các phương trình sau: LG a sin3x−cos5x=0sin3x−cos5x=0 Phương pháp giải: B1: chuyển vế, đưa PT về dạng sinα=cosβsinα=cosβ. B2: Do sinx=cos(π2−x)sinx=cos(π2−x) PT trở về dạng cosX=cosYcosX=cosY với X=(π2−x);Y=βX=(π2−x);Y=β ⇔[X=Y+k2πX=−Y+k2π(k∈Z)⇔[X=Y+k2πX=−Y+k2π(k∈Z) Từ đó suy ra nghiệm x và KL. Lời giải chi tiết: sin3x−cos5x=0⇔cos5x=sin3x=cos(π2−3x)⇔[5x=π2−3x+k2π5x=−π2+3x+k2π⇔[8x=π2+k2π2x=−π2+k2π⇔[x=π16+kπ4x=−π4+kπ(k∈Z)sin3x−cos5x=0⇔cos5x=sin3x=cos(π2−3x)⇔[5x=π2−3x+k2π5x=−π2+3x+k2π⇔[8x=π2+k2π2x=−π2+k2π⇔[x=π16+kπ4x=−π4+kπ(k∈Z) Vậy nghiệm phương trình là: x=π16+kπ4(k∈Z)x=π16+kπ4(k∈Z) và x=−π4+kπ,(k∈Z) Cách khác: sin3x - cos5x = 0
Vậy nghiệm phương trình là: x=π16+kπ4(k∈Z) và x=−π4+kπ,(k∈Z) LG b tan3xtanx=1 Phương pháp giải: B1: Tìm ĐKXĐ. B2: vì 1tanx=cotx=tan(π2−x) phương trình trở về dạng tanα=tanβ với α=3x;β=π2−x ⇔α=β+kπ(k∈Z) B3: Suy ra nghiệm x rồi KL. Lời giải chi tiết: Điều kiện: {cos3x≠0cosx≠0⇔{3x≠π2+kπx≠π2+kπ⇔{x≠π6+kπ3x≠π2+kπ⇒x≠π6+kπ3(k∈Z) tan3xtanx=1⇔tan3x=1tanx⇔tan3x=cotx⇔tan3x=tan(π2−x)⇔3x=π2−x+kπ⇔4x=π2+kπ⇔x=π8+kπ4(k∈Z)(tm) Vậy nghiệm phương trình là x=π8+kπ4,k∈Z. Chú ý: Ở bài này ta thấy ngay họ nghiệm x=π8+kπ4,k∈Z không có nghiệm nào vi phạm điều kiện xác định nên ta lấy cả họ nghiệm và không phải loại bỏ điểm nào. HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|