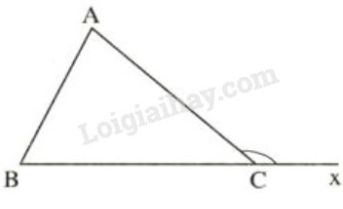
Bài 68 trang 141 SGK Toán 7 tập 1Các tính chất sau đây được suy ra trực tiếp từ định lí nào? Đề bài Các tính chất sau đây được suy ra trực tiếp từ định lí nào? a) Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. b) Trong một tam giác vuông, hai góc nhọn phụ nhau. c) Trong một tam giác đều, các góc bằng nhau. d) Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng tính chất của tam giác cân và định lí về tổng ba góc của một tam giác. Lời giải chi tiết Các tính chất ở các câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng ”. Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”. Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”. * Chứng minh: a)
Ta có: Tổng ba góc của tam giác bằng nên Góc là góc ngoài của tam giác nên Do đó: . b) Tam giác vuông tại Áp dụng định lí tổng các góc của một tam giác vào ta có: c) Giả sử có tam giác đều cân tại và cân tại . (tính chất tam giác cân) d) Giả sử có Có cân tại , do đó . Có cân tại do đó là tam giác đều.
|