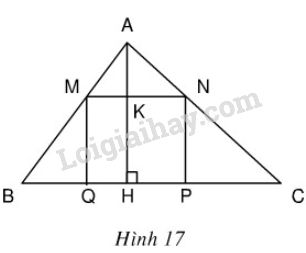
Bài 66 trang 64 SGK Toán 9 tập 2Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm... Đề bài Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Giải bài toán bằng cách lập phương trình Bước 1: Lập phương trình 1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm) 2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết 3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận. Chú ý: Dựa vào tỉ lệ cạnh của tam giác đồng dạng để tính các cạnh cần thiết. Sử dụng công thức tính diện tích hình chữ nhật bằng tích của chiều dài với chiều rộng. Lời giải chi tiết Gọi \(x\) (cm) là độ dài của đoạn \(AK\). Điều kiện \(0 < x < 12\) Vì \(∆ABC\) đồng dạng \(∆AMN\) nên \(\eqalign{ Ta có: \(MQ = KH = 12 – x\) Do đó diện tich hình chữ nhật \(MNPQ\) là: \(\displaystyle \left( {12 - x} \right){{4{\rm{x}}} \over 3}\) Ta có phương trình: \(\displaystyle \left( {12 - x} \right){{4{\rm{x}}} \over 3} = 36 \Leftrightarrow {x^2} - 12{\rm{x}} + 27 = 0\) Phương tình trên có \( \Delta'=(-6)^2-1.27=9>0\) Suy ra \({x} = 9\) (nhận) hoặc \({x} = 3\) (nhận) Vậy độ dài của đoạn \(AK = 3cm\) hoặc \(AK=9cm\). Suy ra \( \dfrac {AM}{AB}=\dfrac {1}{4}\) hoặc \( \dfrac {AM}{AB}=\dfrac {3}{4}\) Khi đó \(M\) sẽ có hai vị trí trên \(AB\) nhưng diện tích hình chữ nhật \(MNPQ\) luôn bằng \(36\) cm2 HocTot.Nam.Name.Vn
|